Double Angle Triples

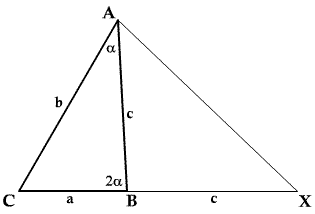
Consider the triangle $ABC$ as shown in the diagram. Show that if $\angle B = 2 \angle A$ then $b^2=a^2+ac$. Find integer solutions of this equation (for example, $a=4$, $b=6$ and $c=5$) and hence find examples of triangles with sides of integer lengths and one angle twice another.

This problem was solved by Yatir Halevi, of Maccabim-Reut High School, Israel. He found a general parametric formula for triangles where one angle is twice another that gives the lengths of the sides $a$, $b$ and $c$ (all integers) of such triangles. The angle opposite side $b$ is double the angle opposite side $a$. Choosing different values of the parameters $u$ and $v$ you get triangles given by:

$$a=u^2, \quad b=uv, \quad c=v^2-u^2.$$

First you have to prove the identity $b^2=a^2+ac$ for such triangles. It can be proved using the similar triangles in the diagram or alternatively from the Sine and Cosine Rules.

Method 1
By construction $\Delta ABX$ is an isosceles triangle. The angle of this triangle at $B$ is $180^\circ - 2\alpha$, and hence the angles at $A$ and $X$ are $\alpha$. Therefore $\Delta XAC$ and $\Delta ABC$ are similar; hence

$${a\over b} = {BC\over AC} = {AC\over XC}={b\over a+c},$$

and thus $b^2=a^2+ac$.

Method 2
By the Cosine Rule:

$$\eqalign{ b^2 &= a^2 + c^2 -2ac \cos 2\alpha \cr a^2 &= b^2 + c^2 -2bc\cos \alpha }$$

Subtracting the equations, using the double angle formula and rearranging them a bit we get :

$$2b^2 - 2a^2 = 2c(b\cos \alpha - a\cos ^2\alpha +a).\quad (1)$$

By the Sine Rule:

$$\eqalign{ {a\over \sin \alpha }&= {b \over \sin 2\alpha } \cr {a \over \sin \alpha } &= {b \over 2\sin \alpha \cos \alpha } \cr \cos \alpha &= {b\over 2a}. \quad (2)}$$

Combining (1) and (2):

$$\eqalign{ 2b^2 - 2a^2 &= 2c({b^2\over 2a} - {2ab^2 \over 4a^2} + a) \cr &= 2c({b^2\over 2a} - {b^2\over 2a} + a) \cr b^2 - a^2 &= ca \cr b^2 &= a^2 + ac.}$$

To find integer solutions, we may assume that $a$, $b$ and $c$ have no common factors. Then $a$ and $a+c$ have no common factors (for if $p$ divides $a$ and $a+c$ then it divides $c$, and hence also $b$). As $a(a+c)=b^2$, and as $a$ and $a+c$ are coprime, $a$ and $a+c$ must be perfect squares. Let $a=u^2$, $a+c=v^2$ so that

$$a=u^2, \quad b=uv, \quad c=v^2-u^2.$$

Note that not every solution gives rise to a triangle (for all three triangle inequalities must be satisfied); for example, $u=1$ and $v=4$ gives $(a,b,c) = (1,4,15)$ and this does not give a triangle. The following are a few examples of values which do give triangles:

u	v				a	b	c
2	3				4	6	5
3	4				9	12	7
3	5				9	15	16
4	5				16	20	9

Note: it can be proved that $a$, $b$ and $c$ give a triangle if and only if $v > u > v/2$; see Math. Gazette , Vol. 412, June 1976, p.130.