Double Angle Triples
Problem
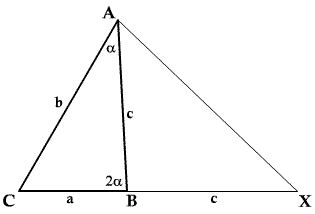
Consider the triangle $ABC$ as shown in the diagram. Show that if $\angle B = 2 \angle A$ then $b^2=a^2+ac$. Find integer solutions of this equation (for example, $a=4$, $b=6$ and $c=5$) and hence find examples of triangles with sides of integer lengths and one angle twice another.
Getting Started
Consider the triangle $ABC$ as shown in the diagram. Use similar triangles to show that if $\angle B = 2 \angle A$ then $b^2=a^2+ac$.
To find integer solutions of this equation, consider the factors of $a(a+c)=b^2$, and that $a$ and $a+c$ have no common factors, so $a$ and $a+c$ must be perfect squares. This will lead to a parametric representation of $a$, $b$ and $c$ in terms of two parameters and you can use this to generate the triples.
Student Solutions
Consider the triangle $ABC$ as shown in the diagram. Show that if $\angle B = 2 \angle A$ then $b^2=a^2+ac$. Find integer solutions of this equation (for example, $a=4$, $b=6$ and $c=5$) and hence find examples of triangles with sides of integer lengths and one angle twice another.
This problem was solved by Yatir Halevi, of Maccabim-Reut High School, Israel. He found a general parametric formula for triangles where one angle is twice another that gives the lengths of the sides $a$, $b$ and $c$ (all integers) of such triangles. The angle opposite side $b$ is double the angle opposite side $a$. Choosing different values of the parameters $u$ and $v$ you get triangles given by:
$$a=u^2, \quad b=uv, \quad c=v^2-u^2.$$

First you have to prove the identity $b^2=a^2+ac$ for such triangles. It can be proved using the similar triangles in the diagram or alternatively from the Sine and Cosine Rules.
Method 1
By construction $\Delta ABX$ is an isosceles triangle. The angle of
this triangle at $B$ is $180^\circ - 2\alpha$, and hence the angles
at $A$ and $X$ are $\alpha$. Therefore $\Delta XAC$ and $\Delta
ABC$ are similar; hence
$${a\over b} = {BC\over AC} = {AC\over XC}={b\over a+c},$$
and thus $b^2=a^2+ac$.
Method 2
By the Cosine Rule:
$$\eqalign{ b^2 &= a^2 + c^2 -2ac \cos 2\alpha \cr a^2 &=
b^2 + c^2 -2bc\cos \alpha }$$
Subtracting the equations, using the double angle formula and
rearranging them a bit we get :
$$2b^2 - 2a^2 = 2c(b\cos \alpha - a\cos ^2\alpha +a).\quad
(1)$$
By the Sine Rule:
$$\eqalign{ {a\over \sin \alpha }&= {b \over \sin 2\alpha } \cr
{a \over \sin \alpha } &= {b \over 2\sin \alpha \cos \alpha }
\cr \cos \alpha &= {b\over 2a}. \quad (2)}$$
Combining (1) and (2):
$$\eqalign{ 2b^2 - 2a^2 &= 2c({b^2\over 2a} - {2ab^2 \over
4a^2} + a) \cr &= 2c({b^2\over 2a} - {b^2\over 2a} + a) \cr b^2
- a^2 &= ca \cr b^2 &= a^2 + ac.}$$
To find integer solutions, we may assume that $a$, $b$ and $c$ have
no common factors. Then $a$ and $a+c$ have no common factors (for
if $p$ divides $a$ and $a+c$ then it divides $c$, and hence also
$b$). As $a(a+c)=b^2$, and as $a$ and $a+c$ are coprime, $a$ and
$a+c$ must be perfect squares. Let $a=u^2$, $a+c=v^2$ so that
$$a=u^2, \quad b=uv, \quad c=v^2-u^2.$$
Note that not every solution gives rise to a triangle (for all
three triangle inequalities must be satisfied); for example, $u=1$
and $v=4$ gives $(a,b,c) = (1,4,15)$ and this does not give a
triangle. The following are a few examples of values which do give
triangles:
| u | v | a | b | c | |||
| 2 | 3 | 4 | 6 | 5 | |||
| 3 | 4 | 9 | 12 | 7 | |||
| 3 | 5 | 9 | 15 | 16 | |||
| 4 | 5 | 16 | 20 | 9 |
Note: it can be proved that $a$, $b$ and $c$ give a triangle if and only if $v > u > v/2$; see Math. Gazette , Vol. 412, June 1976, p.130.
