Little Boxes
How many different cuboids can you make when you use four CDs or DVDs? How about using five, then six?
Problem
I don't know whether you've had the same problem as me. I've found that I have loads of CDs and DVDs and they are not very tidy. I decided to collect them all together in their boxes and after putting them all the same way up I started putting them together into cuboid-type shapes. I found when I started that just two could be put together to give three different cuboids. Here's what they looked like:-

I've used different colours to show each box, just to make it clearer to see, but we're going to imagine each box is identical.
I then tried it with an extra box making three altogether. I moved them around and found that again I could make three different cuboids. These are the ones that I found:-

But, perhaps like you, I've got lots of these boxes of CDs and DVDs. So I moved on to using four. Again I found three but realised that there were more that I could find. Here are the three:-

Well, you could try the same ideas. If you have not got CD/DVD boxes it does not matter. You could use old match boxes or books that are all the same size. In fact you can use any objects as long as they are cuboid shaped and you have plenty of them that are exactly the same. All you have to do is to find out how many different cuboids you can make when you use fourof them, then five of them, then six etc.
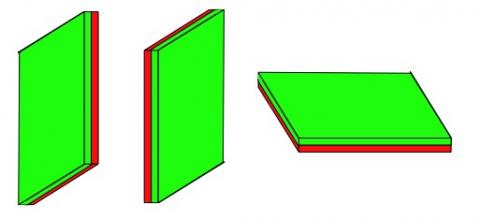
But notice that when you've put them together it does not matter which way up they are, they count as being the same. For example these three would count as being the same:-
Now that you've tried some, how about getting other friends and people at home to have a go and see what they all come up with - maybe you could work together?
Well, Good Luck.
Getting Started
How will you know you have found all the different ways?
It might help to describe how you have put the boxes together to someone else.
Are there any faces which you haven't joined together?
Student Solutions
No real ideas came forward as to what people did get from this exploration. We are interested in any work that proceeds from looking at the challenges - so, let us know if you can.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
For more extension work
Possible support
