Strange Rectangle 2
Problem
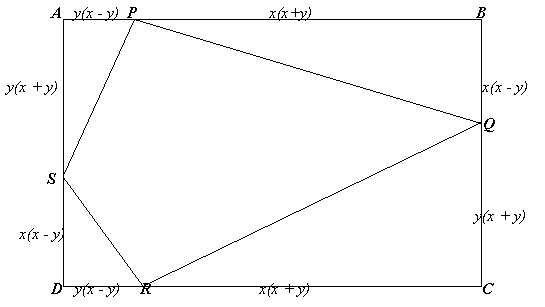
As $x$ and $y$ change the points $S$, $P$, $Q$ and $R$ always lie on the circle with $SQ$ as diameter and the angles of the quadrilateral $SPQR$ remain the same. (See the problem Strange Rectangle from November 2001.)
Taking
$x = \sqrt{3}$ and $y = 1$
find all the angles in this figure and the exact values of the sine, cosine and tangent of these angles in surd form.Now take
$x = \sqrt{2} + 1$ and $y = 1$
and find the exact values of the trigonometric ratios for $22.5^o$ and $67.5^o$Getting Started
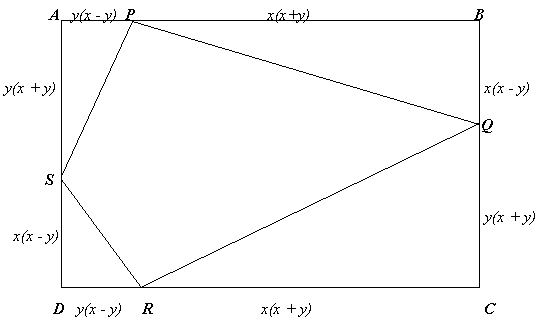
From the solution to the problem Strange Rectangle (November 2001) you know angles $SPQ$ and $SRQ$ are right angles, angle $PQR$ is 45 degrees and angle $PSQ$ is 135 degrees.
For the first part you need to know
$ \tan 60^{\circ} = \sqrt3$
When you take $x=\sqrt 3$ and $y=1$ and use the triangles in the diagram you can find the exact values of the sine, cosine and tangent of these angles in surd form.
Look carefully at $AS$ and $SD$ for the second part. Here you take $x=\sqrt 2 + 1$ and $y=1$ to find the exact values of the trigonometric ratios for $22.5$ degrees and $67.5$ degrees.
Student Solutions
David provided us with his solution:

I firstly used the angles calculated in *** and put them on the diagram. Next I used the fact that $ \sin30=1/2$ (this isn't too difficult to prove), to find that $z=30$ degrees. From this, I could work out all the other angles and fill them in:
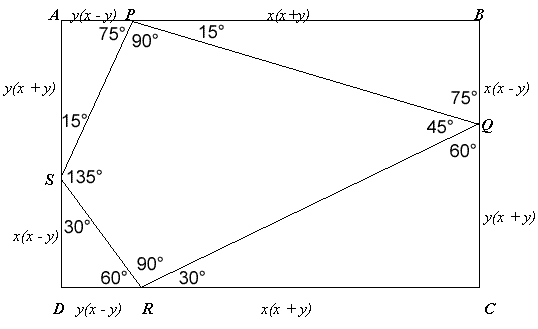
from this all the sine, cosine and tangent values can be read off.
For the final part, I noticed when
$x = \sqrt{2} + 1$ and $y = 1$ then $SD$ and $AS$ are the same length. This makes $SDR$ and $SAP$ similar triangles, and so the angle $DSR$ is $22.5$ degrees. So we get:
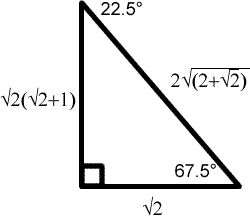
From which all the sine, cosine and tangent values of $22.5$ degrees can be obtained.
