3 rings
Problem
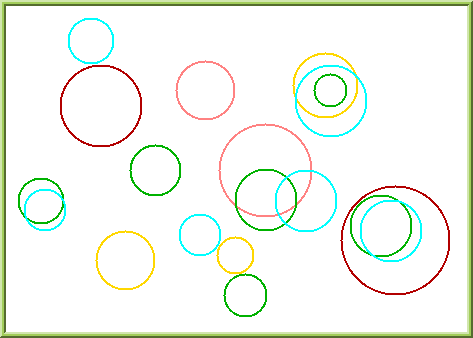
I found a number of small bracelets and rings on a table some time ago and I noticed how some were on their own, others were touching at the edges, others were overlapping each other and some small ones had found themselves inside larger ones.
Image
|
Image
|
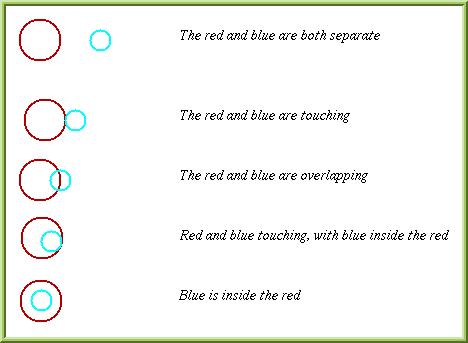
I took two of these, one ring and one bracelet, and explored what possibilities there were. |
I thought that this would be the next challenge for you all. To look at the situation when you have three rings, circles, bracelets . . . . it doesn't matter what they are really or what size they are. They could even expand and get bigger or get smaller if you liked. But, thinking of the four things I noticed at the start:-
1) TOUCHING
2) OVERLAPPING
3) SEPARATE
4) IN/OUT SIDE
I wonder what would be the number of ways in which 3 such circles could be?
Here are some ways, remember I said they could be different sizes each time, but I've coloured them so that it is easy to know which one we are talking about.

Well I feel you could carry on at this point, just a few points to remember:-
When writing you must say something about each of the three circle/rings/bracelets.
Three separate ones could be anywhere yet separate and they would all count as one arrangement, and the same kind of things goes for any other arrangement, if the words are the same then, for this challenge the arrangement is the same.
You could now ask "I wonder what would happen if.....?"
Getting Started
Student Solutions
We haven't had any solutions to this investigation yet and you might have gone down many different routes. However, if you discover anything interesting, please do let us know by emailing primary.nrich@maths.org . Please don't worry that your solution is not "complete" - we'd like to hear about anything you have tried. Teachers - you might like to send in a summary of your children's work.
