Golden Triangle
Three triangles ABC, CBD and ABD (where D is a point on AC) are all isosceles. Find all the angles. Prove that the ratio of AB to BC is equal to the golden ratio.
Problem
Image
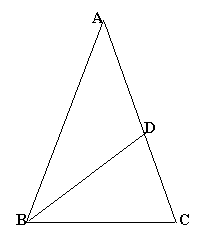
The three triangles $ABC$, $CBD$ and $ABD$ are all isosceles. Find the angles in the triangles.
The sides $AB$ and $BC$ have lengths $p$ and $q$ respectively. Prove that the ratio $p/q$ is equal to the golden ratio $\frac{1}{2} (\sqrt{5}\ +1) $.
and find the ratio $q/p$.The area of triangle $ABC$ is 2 square units. Find the areas of $CBD$ and $ABD$ exactly (i.e. find the areas in the form \[ a + b \sqrt{5} \]
where $a$ and $b$ are rational numbers)Student Solutions
| The three triangles are all isoceles so $ \angle BDC = \angle ACB = \angle ABC. $ |
Image

|
$ \angle BDC = \angle BAC + \angle DBA = 2 \angle BAC. $
$ \angle BCD + \angle ABC + \angle BAC = \angle BDC + \angle
BDC + \angle BAC = 180^o. $
$ 2 \angle BAC + 2 \angle BAC + \angle BAC = 180^o $
$ 5 \angle BAC = 180^o $,
$ \angle BAC = \angle DBA = 36^o$,
$\angle BDA = 108^o $ ,
$ \angle ABC = \angle ACB = \angle BDC = 72^o $
and $ \angle CBD = 36^o. $
The triangles $ ABC $ and $ BDC $ have lengths $ AB = AC = p $
and $ BC = BD = DA = q $ and the angles are $ 36^o , 72^o $ and $
72^o $ so they are similar triangles. Taking the ratio of
corresponding sides $ AC/BC = BC/DC $ : $$\frac{p}{q} =
\frac{q}{p-q}$$ So $ p^2 -pq-q^2 = 0 $ and dividing by $ q^2 $
gives the quadratic equation $$(p/q)^2 -(p/q)-1=0 $$ which has the
solutions $(1 \pm \sqrt 5) /2$. We don't want the negative root for
such a ratio as it would make no sense. Hence $ p/q = (\sqrt{5} +
1)/2 $. Similarly $ q/p = (\sqrt 5 - 1)/2 $.
Triangles $ ABC $ and $ BDC $ are similar and the ratio of
areas is the square of the ratio of corresponding sides. So area
of
$ BDC : ABC $ $ = [(\sqrt 5 - 1)^2/2 ] : 1 $
$ = (6 -2\sqrt 5 )/4 : 1 $
$ = (3 - \sqrt 5 ) : 2 $
So if the area of triangle $ ABC $ is $2$ the area of triangle
$ BDC $ is $3-\sqrt 5$ and the area of triangle $ ABD $ is $ 2 - (3
- \sqrt 5) = \sqrt 5 -1 $.
