Quadarc
Problem
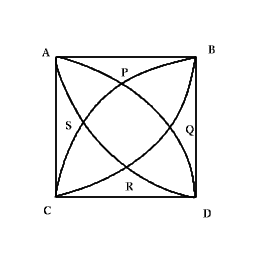
Given a square $ABCD$ of sides $10$ cm, and using the corners as centres, construct four quadrants with radius $10$ cm each inside the square. The four arcs intersect at $P$, $Q$, $R$ and $S$. Find the area enclosed by $PQRS$.
Student Solutions
The solution below was done by Arun Iyer, age 17, S.I.A Junior College, South Indian Assoiate, Nr Station Dombivli (W), Thane Di 421 202, India and similar solutions were sent in by Tony Cardell and John Lesieutre, age 14, from State College Area High School, Pennsylvania, USA.
Given a square $ABCD$ of sides 10 cm, and using the corners as centres, construct four quadrants with radius 10 cm each inside the square. The arcs intersect at $P$, $Q$, $R$ and $S$ and we have to find the area $PQRS$ enclosed by the arcs.
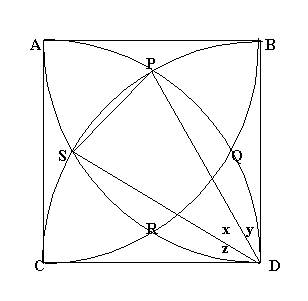
Consider triangles $CPD$ and $SBD$. Both are equilateral triangles. ($CP = PD = CD$ = 10cm and $SB = SD = BD$ = 10cm). Therefore from the diagram \(x+y = 60^\circ \) and \(x+z = 60^\circ \). We know that \(x+y+z= 90^\circ \) so from these three equations,
\(x= 30^\circ =\pi /6\). The area of segment $PS$ = area of sector $PDS$ - area of triangle $PDS$. Call this area \( \Delta \)
\[\Delta = {1 \over 2}(10)^2 (x - \sin x). \]
By symmetry, there are 4 such equal segments. Hence, the total area of the segments is \(4\Delta.\)
Since the angles subtended by the arcs $PQ$, $QR$, $RS$ and $PS$ are equal, we get chords $L(PQ) = L(QR) = L(RS) = L(PR)$.
We can find $L(PS)$ by applying the cosine rule to triangle $PDS$, \[L(PS)^2 = (10)^2 + (10)^2 - 2(10)^2 \cos x = 2(10)^2(1 - \cos x).\] \[\mbox{Area of square $PQRS$} = L(PS)^2 = 2(10)^2(1 - \cos x).\]
The required area of $PQRS$ = area of 4 segments + area of square $PQRS$.
$$\eqalign{ {\rm Area} &= 200(x - \sin x) + 200(1 - \cos x) \cr &= 200({\pi \over 6} - \sin{\pi \over 6} + 1 - \cos {\pi \over 6}) \cr &= 200({\pi \over 6} - {1\over 2}+ 1 - {\sqrt 3 \over 2})\cr &= 100(1 + {\pi \over 3} - \sqrt 3) \cr &= 31.54 \ {\rm cm^2 (rounded \ to \ 4 \ significant\ figures.)} }.$$