Long Short
Problem

Label the sides: $a$ is the shortest, $b$ is the next shortest, then $c$, and finally $d$ is the longest side (it is possible to have two sides of equal length).
What is the maximum length that the shortest side $a$ could be?
Side $b$ must be less than a certain value - what value?
What is the maximum length that the longest side $d$ could be? Is it possible for $c$ and $d$ both to be this maximum length?
Student Solutions
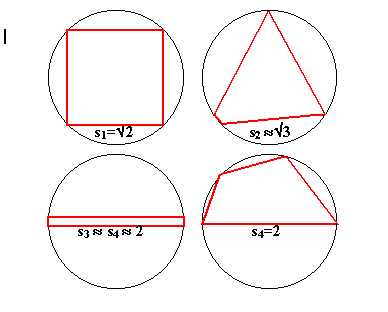
This solution is from Tony Cardell, age 15, State College Area High School, PA, USA.
We investigate quadrilaterals inscribed in the unit circle. The sides of the quadrilateral $s_1$, $s_2$, $s_3$, $s_4$, subtend angles $\theta_1, \theta_2, \theta_3, \theta_4$ at the centre of the circle where $\theta_1 \leq \theta_2 \leq \theta_3 \leq \theta_4$. Now $\theta_1 \leq 90^\circ$ so the the largest value of
$s_1$ is when the quadrilateral is a square.First investigating an inscribed quadrilateral where all sides are equal, $s = s_1 = s_1 = s_3 = s_4$ , which is a square with diagonal of length 2 units, we find that the side length of this square is given by $2s^2 = 4$, so that
\( s = \sqrt{2}\).
If we made $s_1$ any larger, clearly the larger square that is formed will not fit in the circle.Now imagine an equilateral triangle inscribed in the unit circle. The angle at the centre is \(120^\circ \)
and the side length is \( s = \sqrt{3}\) . We can make a quadrilateral by slightly distorting this triangle and introducing another very short side. Therefore, in our quadrilateral, the second side must always be less than \( s = \sqrt{3}\) since if not side one would have length zero and you would not have a quadrilateral. However side one can get very small, approaching zero, so that side 2 can approach \( s = \sqrt{3}\) . We can have one very short side (almost zero) one just less that \( s = \sqrt{3}\) and the other two equal to \( s = \sqrt{3}\) .Side 3 can approach length 2 because we can make a quadrilateral with sides three and four very close to 2 and sides one and two very close to zero. As sides one and two approach zero, sides three and four clearly approach 2, the diameter of the unit circle.
Finally, at its maximum, side 4 can be 2 when side 4 is the diameter of the unit circle. The other sides will fit into one of the halves of the circle because you can make them as small as you want. Any line longer than 2 units will extend outside the circle so side four cannot be longer than 2 units.
Teachers' Resources
Why do this problem?
Possible approach
The last part of the question encourages discussion along similar lines. It is good to bring out of the discussion that the third side can be as close to $2$ units as you wish but can never actually be exactly $2$.
