There's a Limit
Problem
Explore the continued fraction:
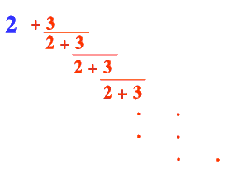
What do you notice when successive terms are taken? What happens to the terms if the fraction goes on indefinitely?
Student Solutions
Tony of State College Area High School, Pennsylvania, USA and Chi Kin of Saint Dominic's International School, Lisbon sent in excellent solutions and here is Chi Kin's:
What happens when successive terms are taken in the continued fraction
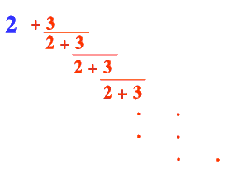
I calculated the first five terms
$2 + {3\over2} = {7\over2} = 3.5 $
$2 + \frac{3}{2+{3\over2}} = {20\over7} = 2.86 $
The third term is $3.05$
The fourth term is $2.95$
And the fifth term is $3.02$
Thus, when successive terms are taken, the results oscillate alternately above and below $3$.
Indeed, if the fraction goes on forever, we would get $3$.
Suppose the continued fraction is denoted as $F$. Thus
$$\eqalign{ F &=& 2 + \frac{3}{F} \\ F &=& \frac{2F + 3}{F} \\ F^2 - 2F - 3 &=& 0 \\ (F-3)(F+1) &=& 0.}$$Thus $F = 3$, because $F$ cannot be negative.
