Plants
Three children are going to buy some plants for their birthdays. They will plant them within circular paths. How could they do this?
Problem
Uncle Raj has three children. Next year, when they've had their birthdays, Naomi will be $5$, Alex will be $6$ and Chris will be $7$. The family has decided on something rather unusual for part of their presents.
All three children have their birthday in the late spring and since they are keen on gardening they are going to buy some plants for the garden, one for each year they have been alive.
Here is the plan of their house and garden:
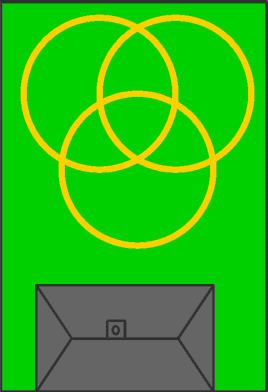
You notice that there are three circular paths that cross over each other. Each child is to have a circle but there will be some bits that are shared, around the middle.
When the time comes, the four of them go off to the garden centre to choose the plants. They do not have a lot of money so they're looking for special offers. They find a very special offer which gives a good discount if you buy ten plants altogether. The three children say that that is no good because they need more than ten. But Uncle Raj realises they can manage with only ten.
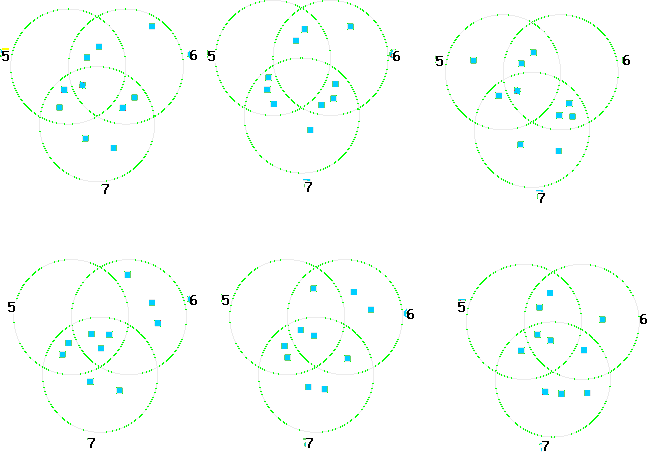
They go to the cafe and have some cool drinks, and Uncle Raj draws a plan of the three paths and puts little marks to show the plants.
Here is his idea:

The children are fascinated to see that Naomi has $1$ and shares $4$, Alex has $2$ and shares $4$ and Chris has $3$ and shares $4$. They think that's rather cool and it saves them a lot of money. So they finish their drinks and off they go to buy their ten plants.
Well now it's your turn to have a go and find some different solutions.
REMEMBER:- You must use exactly ten plants (no more, no less)
REMEMBER:- The circles must contain $5$, $6$ and $7$ plants (no more, no less).
As you try, you may find that you are developing a system for getting the next one. If so, we'd love to hear about it. You might like to try to find them all, and write about all the things you notice about each solution.
You could print off this sheet to help you record them, if you like. However, you might find a different way of recording them altogether. Some people find it's easiest to do it quite large and have ten objects to move around in different places.
As with most of these challenges you can and should ask "I wonder what would happen if ...?" Well you might try a different number of objects (plants). You could try different numbers for each circle, as if the children were different ages.
Good luck and don't forget about sending in any results you have.
You might now like to have a go at More Children and Plants.
Getting Started
How many plants have you got in each circle?
What could you do to make the correct totals?
Student Solutions





Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension


For more extension work
Obvious extension work can be looked at by considering four or more areas - so take yourselves to More Children and Plants.
Possible support
