Orthogonal Circle
Given any three non intersecting circles in the plane find another circle or straight line which cuts all three circles orthogonally.
Problem
Image
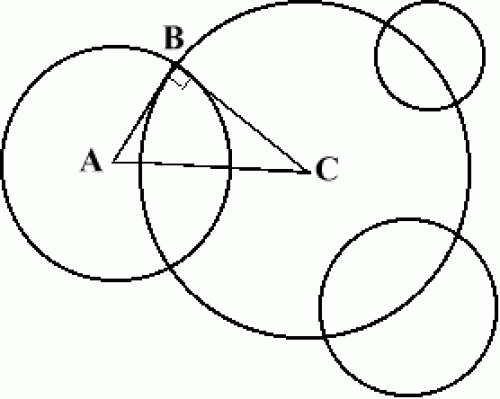
| It is known that given any three non intersecting circles in the plane there is another circle or straight line that cuts the three given circles at right angles. (The circle or straight line is said to be orthogonal to the 3 original circles.)
Given three circles with centres $(0, 0)$, $(3, 0)$ and $(9, 2)$ and radii $5$, $4$ and $6$ respectively find the centre and radius of the circle that cuts the three given circles at right angles. Draw the circles to check that the circle you have found appears to be orthogonal to the others. |
What happens in the case of three circles with centres at $(0, 0)$, $(3, 3)$ and $(8, 8)$ and radii $1$, $2$ and $3$ respectively?
Given three circles, how can you tell without calculating which of the two cases applies, an orthogonal circle or an orthogonal straight line?
Getting Started
Call the centre of the orthogonal circle $(h, k)$ and the radius $r$ (equal to $CA$ in triangle $ABC$). Use Pythagoras' Theorem for triangle $ABC$ to write down an equation. In a similar way find equations using the other two circles.
Student Solutions
Congratulations to Tony from State College Area High School, Pennsylvania, USA for this solution.
First of all, here is the solution to finding the equation of the orthogonal circle for the circles with centers of $(0,0)$, $(3,0)$, $(9,2)$ and radii respectively of $5$, $4$, and $6$.
As the circles are orthogonal we can draw three right angled triangles. One of the legs of each right triangle is the radius of one of the given circles, the other leg is the radius of the unknown orthogonal circle, and the hypotenuse is the distance between the center of the known circle and the center of the unknown orthogonal circle.
Teachers' Resources
Why do this problem?
The problem naturally brings in the formula for a circle and it could be used to introduce this formula.
The problem requires knowledge and understanding of the formula for the distance between two points, the use of Pythagoras Theorem and algebraic skills in solving simultaneous equations.
The problem introduces the concept of orthogonality which is very important in higher mathematics.
Possible approach
Depending on their experience of problem solving and thinking for themselves, if there is some lack of confidence then the class could first discuss how they are going to set about solving the problem. This should be in the context of the teacher making it explicit that the learners should be developing problem solving skills and growing out of dependence on the teacher to indicate methods to use.
- List what information is given, what they are trying to find, and then how to use the information given.
- In trying to find the orthogonal circle the 3 unknowns are its radius and the coordinates of its centre.
- The diagram suggests the use of 3 right angled triangles and the use of Pythagoras' Theorem to give 3 equations.
- How can they solve the equations. How can they eliminate one of the variables between pairs of equations.
The learners can then work independently having planned how to work on the problem.
Key questions
What information is given in the question?
What are the unknowns? Have we assigned notation to refer to the unknowns?
Can we use the given information, and our mathematical knowledge, to write down some equations?
What methods have we used in the past to solve similar equations? Are those methods useful here?
