Snooker Frames
It is believed that weaker snooker players have a better chance of winning matches over eleven frames (i.e. first to win 6 frames) than they do over fifteen frames. Is this true?
Problem

A single game of snooker is called a frame. In the first round of a snooker tournament, the matches are played over eleven frames (so the first player to win six frames wins the match). In the later rounds matches are played over 15 frames. Assume that each player has steady nerves and his chance of winning any frame (irrespective of who starts) is constant.
In the problem Snooker you were asked to find the probability that a player wins a match over fifteen frames, given that his chance of winning any frame is $0.4$. You should now find the probability that this player wins a match over eleven frames.
It is believed that the weaker players have a better chance of winning the matches over eleven frames than they do over fifteen frames. Do your results confirm this or not?
Does this surprise you, or not? Why?
Getting Started
The method for solving this problem is given in the solution to the problem Snooker.
You have to compare the probabilities of winning a match which is the best out of 11 frames with one that is the best out of 15 frames. In the first case the first player to win 6 frames wins the match and in the second case the first to win 8 frames wins the match.
Assume that each player has steady nerves and his chance of winning any frame (irrespective of who starts) is constant.
You can use the results in the problem Snooker for the probability that a player wins a match over 15 frames, given that his chance of winning any frame is $0.4$. All you have to do here is to use a similar method to work out the probability that this player wins a match over 11 frames. It is believed that the weaker players have a better chance of winning the matches over eleven frames than they do over fifteen frames. Do your results confirm this or not?
Student Solutions
Ben has solved this Tough Nut. He did not say which school he comes from.
The probability of winning a 15 frame match was shown in the problem Snooker to be $0.2131$ for a weaker player who has a consistent probability of $0.4$ of winning each single frame. We use the same method here.
To win an 11 frame match the player must be the first one to win 6 frames. He may win 6 games outright or win any 5 of the first 6 games and lose one then win one, or any 5 of the first 7 games and lose 2 then win one, or any 5 of the first 8 games and lose 3 then wins one or any 5 of the first 9 games and lose 4 then win one or any 5 of the first 10 games and lose 5 then win one. The probability is $$p^6 + {6\choose 5}p^5(1-p)p + {7 \choose 5}p^5(1-p)^2p + {8 \choose 5}p^5(1-p)^3p+{9\choose 5}p^5(1-p)^4p+ {10 \choose 5}p^5(1-p)^5$$ For $p=0.4$ and $1-p=0.6$ this becomes $$0.4^6[1 + 6 \times 0.6 + 21 \times 0.6^2 + 56 \times 0.6^3 + 126 \times 0.6^4 + 252 \times 0.6^5 = 0.2465018$$ As $0.2465 > 0.2131$ this result gives evidence that weaker players are more likely to win 11 frame matches than they are to win 15 frame matches.
James from Bay House school did a numerical investigation and showed that the chances of winning the tournament were very slight with a 0.4 chance of winning each frame.
Even with a 40% chance of winning each frame, the chance of being the first to 18 frames is less than 1 in 10 million!
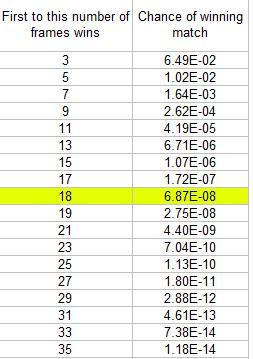
We can also look at the chance of being the first to 18 frames for different probabilities of winning each frame.
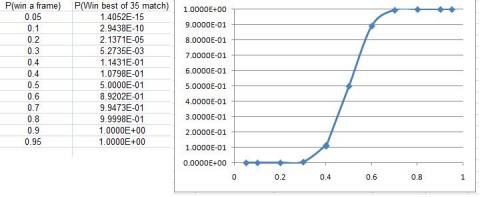
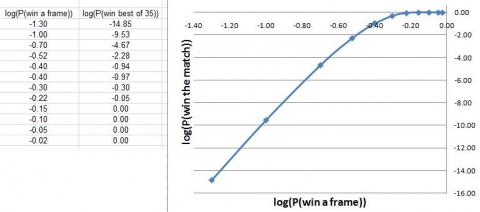
If you plot a log-log graph then you can see a highly linear relationship for values of probability less than about $90$ percent.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
