Without Calculus

Given that $u > 0$ and $v > 0$ what is the smallest possible value of $1/u + 1/v$ given that $u + v = 5$?

Here is a solution from Danny of Milliken Mills High School, Canada.

Let $S$ be the mininum value,

$S = 1/u + 1/v = (v + u)/(uv)$.

Since $u + v = 5$ then $S = 5/uv$.

The maximum value of $uv$ gives a mininum value of $S$. Given $u + v = 5$ then $v = 5 - u$.

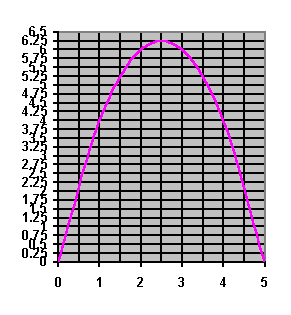
Let $f(u)$ give the value of $uv$ as $u$ and $v$ change. Then $ f(u) = u(5 - u) = -u^2 + 5u $. This is a quadratic function and the vertex $(u, M)$ of the graph of $f(u)$ is at $(2.5, 6.25)$. It means the maximum value occurs at $M = 6.25$ when $u = 2.5$ and $v = 5 - u = 2.5$. So the mininum value $S = 1/2.5 + 1/2.5 = 0.8$.

Vassil from Lawnswood High School, Leeds used the same method, and drew two graphs to illustrate it, one to show the possible values of $u$ and $v$ where $u + v =5$ and the other, shown below, the graph of $f(u) = u(5 - u) = -u^2 + 5u$ for the corresponding range of values of $u$ and $v$.

Image

Peter and Koopa of Boston College used the Arithmetic Mean - Geometric Mean inequality (AM-GM) noting as above that minimising $1/u + 1/v$ is the same as maximising $uv$. Here is Peter's solution:

From the AM-GM inequality:

arg = $uv \leq [(u+v)/2]^2 = (5/2)^2 = 25/4.$

Hence the minimum value of $1/u + 1/v$ subject to $u+v = 5$, $u$, $v > 0$, is $4/5$.