Cosines Rule
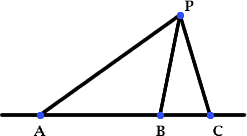
Three points A, B and C lie in this order on a line, and P is any point in the plane. Use the Cosine Rule to prove the following statement.
Problem
(a) Prove that a triangle with sides $3$, $7$, $8$ contains a $60$ degree angle.
(b) Three points $A$, $B$ and $C$ lie in this order on a line, and $P$ is any point in the plane. Use the Cosine Rule to prove that:
\[\frac{AP^2}{AB\cdot AC}+\frac{CP^2}{CA\cdot CB} = 1 + \frac{PB^2}{BA\cdot BC}\]
Getting Started
Why is the $60$ degree angle opposite the side of median length?
For the second part all you need is the cosine formula and some algebraic manipulation to get the required result.
Student Solutions
The Cosine Rule for $\triangle APC$ and $\triangle BPC$, where $\angle ACP=\theta$, gives $$AP^2 = AC^2+PC^2-2AC\cdot PC \cos\theta$$ and $$PB^2= BC^2+PC^2-2BC\cdot PC \cos \theta$$
Hence $$\cos\theta=\frac{BC^2+PC^2-PB^2}{ 2BC\cdot PC}$$ and
$$\cos\theta= \frac{AC^2+PC^2-AP^2}{ 2AC \cdot PC}$$
so we have
$$\frac{BC^2+PC^2-PB^2}{ 2BC\cdot PC}=\frac{AC^2+PC^2-AP^2}{ 2AC \cdot PC}$$ from equating the right-hand sides of these equations.
Multiplying both sides by $\dfrac{2PC}{AB}$ gives
$$\frac{BC^2+PC^2-PB^2}{ BC\cdot AB}=\frac{AC^2+PC^2-AP^2}{ AC \cdot AB}$$ which we can rearrange to obtain
$$\frac{AP^2}{AC.AB} +\frac{PC^2}{AB}\left(\frac{AC-BC}{BC\cdot AC}\right) = \frac{AC-BC}{AB}+ \frac{PB^2}{AB\cdot BC}$$
As $A$, $B$ and $C$ are in a straight line, $AB+BC=AC$, so $AC-BC=AB$. Therefore, we can simplify the previous equation to obtain $$\frac{AP^2}{ AB\cdot AC}+\frac{PC^2}{AC\cdot BC} = 1 + \frac{PB^2}{AB\cdot BC}$$ which is the required result.
Teachers' Resources
Why do this problem?
The first part is an easy application of the cosine rule. The second part requires some algebraic skills and gives practice in proving a formula.
Possible approach
Use as practice. The problem does not require learners to decide on the method to use.
Key questions
Look at the formula to be proved. Write down the cosine formula for the triangles in the diagram using the same notation. Can you see how to manipulate the formulas you have established to give the formula to be proved?
