Tiles on a Patio
Problem
Imagine that round the back of where you live is a piece of ground that your family want to change. Instead of grass or plants growing there you want to have a patio. To prepare to change it the ground is dug up and levelled, it is then measured and found to be a square $10$ by $10$ [this could be feet, metres or yards it does not really matter for this challenge]. You then go to a large store that sells tiles to go on the ground. To your surprise you find that they sell tiles in ten different sizes; $1$ by $1$, $2$ by $2$, $3$ by $3$, etc. up to $10$ by $10$. You decide to go back home for a while and work a few ideas out.
You start by drawing a $10$ by $10$ square; and then you think about what sizes of tiles to use to cover it.
If you use $1$ by $1$ tiles then you find [or know already!] that you will need $100$ of them. So your shopping list would look like :-
$100$ tiles @ $1$ by $1$ > Total number of tiles $100$

If you use $10$ by $10$ tiles then you find [or know already!] that you will need 1 of them. So your shopping list would look like :-
$1$ tiles @ $10$ by $10$ > Total number of tiles $1$
If you use $2$ by $2$ tiles then you find [or know already!] that you will need $25$ of them. So your shopping list would look like :-
$25$ tiles @ $2$ by $2$ > Total number of tiles $25$
You could of course use a mixture of different sized tiles.
If you use $12$ tiles $2$ by $2$ and $4$ tiles $3$ by $3$ and $1$ tile $4$ by $4$ your shopping list would look like :-
$12$ tiles @ $2$ by $2$
$4$ tiles @ $3$ by $3$
$1$ tile @ $4$ by $4$ > Total number of tiles $17$

So you could, with these examples use $1, 17, 25$ or indeed $100$ tiles.
Your challenge starts by asking you to try to find lots of different numbers of tiles that could be used to cover this $10$ by $10$ patio.
You could think about the artistic appearance of it as well if you like. However all the patio must be covered and no cutting any of them to make different sizes or shapes ... they're actually very, very hard to cut anyway.
You could now think about these kinds of questions and perhaps you would think of other questions of your own to pursue.
- Are there some numbers of tiles used that actually are made up of different mixtures of tiles? [For example in our one that used $17$, could you get to use just $17$ tiles but they require a different shopping list from the one above?]
- Are there some numbers between $1$ and $100$ that cannot be used as the total number of tiles required?
- Is there some system for getting new examples that use different numbers of tiles?
You might then think about how all this might or might not change if the patio had been $9$ by $9$ [$8$ by $8$, $7$ by $7$ etc ...]
Well good luck, and if you're artistically inclined I guess that you may have some results that would look really good displayed. Since you're sitting at a computer it may be that you could use a "draw/art" package to do all the work on the screen for you. But have a break from the screen every hour ... your body deserves it!
Getting Started
Using squared paper and drawing your arrangement of tiles might help.
Can you use one of the ways you've already found to find a way using a different number of tiles? Try changing just a part of it, perhaps.
Student Solutions
These solutions are just some examples showing the work of four children.
First of all we have Izzy's examples:-
Image
|
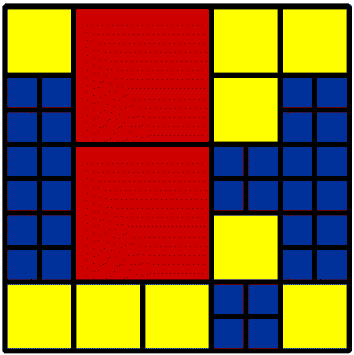
9 2 by 2 2 4 by 4 32 1 by 1 43 Total |
Image

|
96 1 by 1 1 2 by 2 97 Total |
Izzy found that you could not get a solution using 98 or 99 tiles so the next highest after 100 was this one with just 1 2 by 2 replacing 4 1 by 1's.
Now we see Lizzy's:-
Image
|
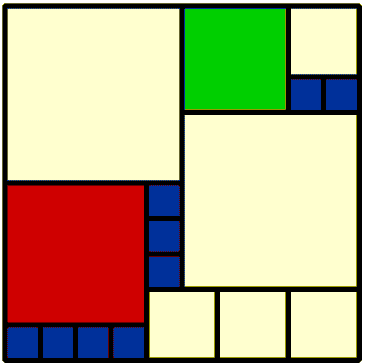
2 5 by 5 1 3 by 3 1 4 by 4 4 2 by 2 9 1 by 1 17 Total |
Image
|
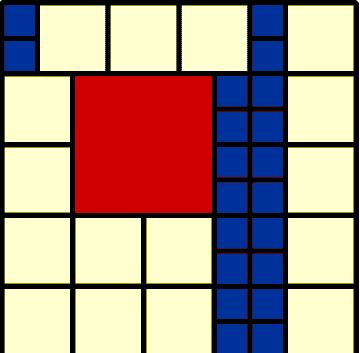
16 2 by 2 20 1 by 1 1 4 by 4 37 Total |
I rather liked her 17 made up of 5 different sizes. The 37 was not symmetrical, many results were, that's neither good nor bad ... it's all O.K.
Then we have Ben:-
Image

|
20 2 by 2 20 1 by 1 40 Total |
Image

|
8 2 by 2 1 6 by 6 32 1 by 1 41 Total |
His 41 would really look good if you wanted it to be very symmetrical. You could probably invent some games in going around the edge from 4 1 by 1's to a 2 by 2. The 40 is interesting because there is the same number of each tile size.
Image
|
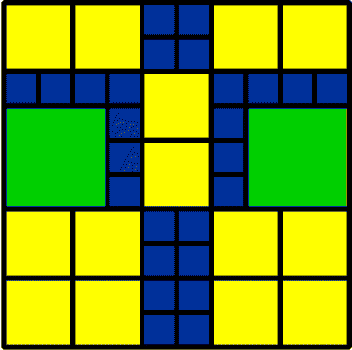
14 2 by 2 2 3 by 3 26 1 by 1 42 Total |
Image
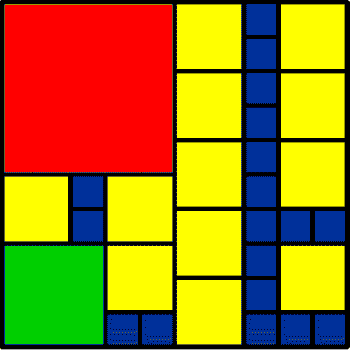
|
12 2 by 2 1 3 by 3 1 5 by 5 18 1 by 1 32 Total |
I think Bo's 42 is rather like a robot! The 32 was very different.
Well done and thank you Izzy, Lizzy, Ben and Bo. Yes these are four real children from the South West of England who were in a group of 19 doing this activity.
