Platonic Planet
Glarsynost lives on a planet whose shape is that of a perfect
regular dodecahedron. Can you describe the shortest journey she can
make to ensure that she will see every part of the planet?
Problem
Image

Glarsynost the alien lives on a platonic planet whose shape is that of a perfect regular dodecahedron.
Every day, she likes to go for a walk to have a look at her planet and see if she has any visitors.
What fraction of the planet's surface can she see from the middle of a face? From an edge? From a vertex?
Her walk needs to start and end at the same place, and she needs to be able to see every part of the planet's surface at some stage during her walk. Investigate the possible paths she could take. The challenge is to find the shortest path you can!
One way of investigating and recording this could be to create a net of a dodecahedron, and draw the path on the net, being careful to consider which faces will join when the net is folded up.
Here are two nets you could use, but you may find it easier to visualise an efficient path using a different one.
Image

Image

Getting Started
How much of the planet's surface can the alien see if she is in the
middle of one of the faces?
What about on one of the edges?
Or at a vertex?
Try to picture a route around the planet either in three dimensions or on a net. Can you be sure every point on the surface is visible from your route? Can you make a more efficient route? Some diagrams might help!
What about on one of the edges?
Or at a vertex?
Try to picture a route around the planet either in three dimensions or on a net. Can you be sure every point on the surface is visible from your route? Can you make a more efficient route? Some diagrams might help!
Student Solutions
Elijah sent us a clear explanation of how he tackled this problem, along with some diagrams showing his solutions.
I made a dodecahedron and made my paths with string and Blu-Tac.
My first assumption was that Glarsynost was not extremely freakishly tall so she can't see over the horizon. Each edge is 1 flib long (a real alien word).
From the middle of a face she can see $\frac{1}{12}$ of the planet. From an edge she can see $\frac{1}{6}$ of the planet. From a vertex she can see $\frac{1}{4}$ of the planet.
FIRST PATH: Start at a vertex and keep going along a new edge so you can see a new face every time. The blue path can be seen in the picture - Path 1. Each face has at least one blue edge. The green lines show edges that are actually joined up to blue ones. The path is 12 flibs long.
Image
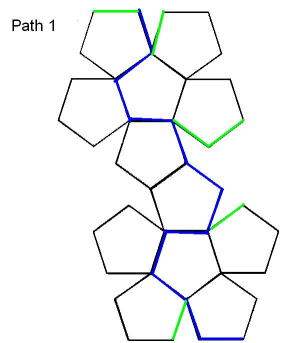
After that I wanted to cut across the faces so the path would be shorter and she could see new faces more quickly. So I wondered how long a diagonal of a pentagon is. My mum told me that it is $\frac{1 + \sqrt5}{2}$ flibs.
SECOND PATH: Start at a vertex and go across a diagonal so you can see two new faces. When you have seen them all, get back to the start. This is Path 2 in the picture. Each face has at least one blue vertex. The path is 6 diagonals long, $3(1 + \sqrt5)$ flibs which is about 9.7 flibs. This is the shortest path I could find, but there are other routes the same length.
Image
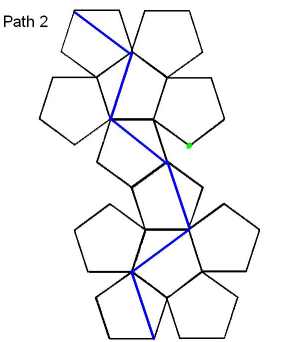
Teachers' Resources
Why do this problem?
This problem gives learners the opportunity to use their
visualisation skills to investigate different paths over the
surface of a solid. Tackling the challenge of finding the shortest
path offers a chance to practise trigonometry, as well as
encouraging justification that there is no better path than the one
they find.
Possible approach
Start with a cube and investigate nets and paths.
How about an octahedron?
Next, ask everyone to imagine they were standing on the
surface of a dodecahedron. Ask what they can see if they are
standing on a face, on an edge, or on a vertex.
One way of introducing the idea of paths on the surface of the
dodecahedron is to have a model of a dodecahedron which can be
drawn on and then unfolded into its net. Alternatively, the path
could be drawn on a net and learners will need to imagine how the
parts of the path will meet up when the net is folded up, to make
sure it really is a closed path.
The pictures of nets shown in the problem are not necessarily
the easiest nets to use to draw the path, so it is worth drawing
out discussion of what would be a good net to use in order to aid
visualisation.
Once everyone is happy with the idea of closed paths on the
surface of the dodecahedron, learners can start to create their own
paths and calculate the lengths. At each stage, they should be
challenging themselves to see whether there is any way they can
make the path shorter while still being able to see every part of
the planet's surface.
In order to compare answers within the classroom, it is
important for the class to decide how long one side of the planet
will be. This could be a good opportunity to discuss the idea of
working things out in terms of a unit length.
Key questions
How much of the planet's surface can I see if I stand at a
face, an edge, a vertex?
Is it easier to investigate this problem using some nets
rather than others?
