Chocolate
There are three tables in a room with blocks of chocolate on each. Where would be the best place for each child in the class to sit if they came in one at a time?
Problem
This challenge is about chocolate. You have to imagine (if necessary!) that everyone involved in this challenge enjoys chocolate and wants to have as much as possible.
There's a room in your school that has three tables in it with plenty of space for chairs to go round. Table $1$ has one block of chocolate on it, table $2$ has two blocks of chocolate on it and, guess what, table $3$ has three blocks of chocolate on it.
Now ... outside the room is a class of children. Thirty of them all lined up ready to go in and eat the chocolate. These children are allowed to come in one at a time and can enter when the person in front of them has sat down. When a child enters the room they ask themself this question:
"If the chocolate on the table I sit at is to be shared out equally when I sit down, which would be the best table to sit at?"

However, the chocolate is not shared out until all the children are in the room so as each one enters they have to ask themselves the same question.
It is fairly easy for the first few children to decide where to sit, but the question gets harder to answer, e.g.
It maybe that when child $9$ comes into the room they see:
- $2$ people at table $1$
- $3$ people at table $2$
- $3$ people at table $3$
"If I go to:
- table $1$ there will be $3$ people altogether, so one block of chocolate would be shared among three and I'll get one third.
- table $2$ there will be $4$ people altogether, so two blocks of chocolate would be shared among four and I'll get one half.
- table $3$, there will be $4$ people altogether, so three blocks of chocolate would be shared among four and I'll get three quarters.
Three quarters is the biggest share, so I'll go to table $3$."
Go ahead and find out how much each child receives as they go to the "best table for them". As you write, draw and suggest ideas, try to keep a note of the different ideas, even if you get rid of some along the way.
THEN when a number of you have done this, talk to each other about what you have done, for example:
A. Compare different methods and say which you think was best.
B. Explain why it was the best.
C. If you were to do another similar challenge, how would you go about it?
Getting Started
How much chocolate is on the first table?
How many people would it have to be shared between?
So, how much chocolate would each person get if you went to the first table?
How about on the second table? ... third table?
Student Solutions
There were a few complete solutions sent in and many who showed us what the final result at the tables would be, i.e. $5$ at the $1$ table, $10$ at the $2$ table and $15$ at the $3$ table.
The full solution showing fractions at each stage were received from Adriel, Emily and Aswaath from the Garden International School in Maylasia. Also Daniel at Staplehurst School and Megan at Twyford School. Here is Emily's contribution.
So after child $9$ has sat down, there are now:
$2$ people at table $1$
$3$ people at table $2$
$4$ people at table $3$
This is a list of which table child $10-30$ would go to:
The reason I listed down which table they would go to is to see whether there was a pattern
Child $10$ would go to table $3$ and receive $ ¾$ of the chocolate
Child $11$ would go to table $3$ and receive $ ½$ of the chocolate
Child $12$ would go to table $2$ and receive $ ½$ of the chocolate
Child $13$ would go to table $3$ and receive $3/7$ of the chocolate
Child $14$ would go to table $2$ and receive $2/5$ of the chocolate
Child $15$ would go to table $3$ and receive $3/8$ of the chocolate
Child $16$ would go to table $1$ and receive $1/3$ of the chocolate
Child $17$ would go to table $3$ and receive $1/3$ of the chocolate
Child $18$ would go to table $2$ and receive $1/3$ of the chocolate
Child $19$ would go to table $3$ and receive $3/10$ of the chocolate
Child $20$ would go to table $2$ and receive $2/7$ of the chocolate
Child $21$ would go to table $3$ and receive $3/11$ of the chocolate
Child $22$ would go to table $1$ and receive $ ¼$ of the chocolate
Child $23$ would go to table $2$ and receive $ ¼$ of the chocolate
Child $24$ would go to table $3$ and receive $ ¼$ of the chocolate
Child $25$ would go to table $3$ and receive $3/13$ of the chocolate
Child $26$ would go to table $2$ and receive $2/9$ of the chocolate
Child $27$ would go to table $3$ and receive $3/14$ of the chocolate
Child $28$ would go to table $1$ and receive $1/5$ of the chocolate
Child $29$ would go to table $2$ and receive $1/5$ of the chocolate
Child $30$ would go to table $3$ and receive $1/5$ of the chocolate
So now there are:
$5$ people in table $1$
$10$ people in table $2$
$15$ people in table $3$
I found out a pattern from child 10 to child $30$. When it was child $16$'s turn to decide which was the best place to sit, child $16$ could just choose to randomly sit on any table because he'll still get $1/3$ of the chocolate in any of the tables. Same with child $22$ and $28$. Child $22$ would either ways get $ ¼$ and child $28 1/5$. The numbers also increase by $6. 16, 22, 28$.
I noticed that sometimes there were tables that shares the same amount of chocolate so you could choose randomly between $2$ or all of the tables which was what I did when I tried finding out how many chocolates each child receives as they go to find the best table for them
For example: Child $16$ gets to choose between any of the $3$ tables because he'll still get $1/3$ of the chocolate in any of the tables.
Martino, Guglielmo, Lorenzo and Virginia at the International School of Turin in Italy sent us a picture of their final solution for 30 children:

Yinyi who goes to the Chinese International School, sent us this picture of the table he made to work on the solution:
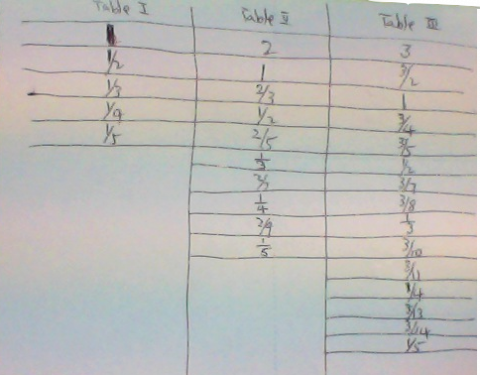
We were sent in several solutions from the children at Clearwater Bay School in Hong Kong - thank you all for sharing your ideas with us. Charlotte and Jasper sent in this table showing their solution:
Well done for working this out! I wonder if anybody can spot the pattern in this solution?
Finally, thank you to Sam and Jack from Orchard Junior School who sent in a table of their solution for a class of 24 children. Sam and Jack chose to represent the fractions of chocolate as decimal numbers but unfortunately, I think you made a little slip-up for the last four pupils in the class.
Well done all of you for your work on quite a difficult challenge.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
For more extension work
These pupils can then move onto the situation of four tables set out with $1, 2, 3, 4$ chocolate bars on them. The two different activities can then be compared, looking at similarities and differences, and giving proofs where appropriate.
Possible support
