On the Road
Problem
Four vehicles travelled on a road with constant velocities.
The car and the scooter were travelling in one direction whilst the bike and the motorcycle travelled in the opposite direction.
The car overtook the scooter at 12:00, then met the bike at 14.00 and the motorcycle at 16.00.
The motorcycle met the scooter at 17.00 then it overtook the bike at 18.00.
At what time did the bike and the scooter meet?
Student Solutions
This solution was sent in by Ben at Madras College in St Andrews. Another good solution was sent in by Nicola at Madras College.
The car overtakes the scooter at 12.00. This point can be taken as the origin of a graph of distance against time.
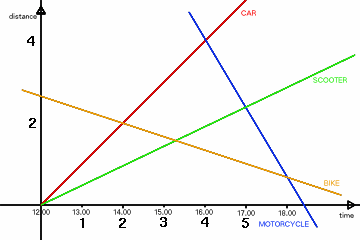
Assuming that the car travels at 1 unit per hour, the car therefore has equation y=x.
Now assume that the scooter travels at $a$ times the speed of the car, where $0 < a < 1$. So, it has equation $y=ax$.
Now for the motorcycle, whose line goes through $(4,4)$ and $(5,5a)$.
Gradient $= (5a-4)/(5-4) = 5a-4$
Substituting in the point $(5,5a)$,
$$ \begin{eqnarray} y - b &=& m(x-a) \\ y - 5a &=& (5a-4)(x-5) \\ y &=& 5ax - 4x - 20a + 20 \end{eqnarray} $$
To find the intersection of the motorcycle and bike, we know that $x=6$.
Therefore $y-5a = (5a-4) \times 1$, and so $y = 10a-4$.
For the bike,
$$ gradient = \frac{10a-4-2}{6-2} = \frac{10a-6}{4} $$
$$ \begin{eqnarray} y -b &=& m(x-a) \\ y - (10a-4)& =& \frac{10a-6}{4}(x-6) \\ 4y - 40a + 16 &=& 10ax - 6x - 60a + 36 \\ 4y &=& 10ax - 6x - 20a + 20 \\ \end{eqnarray} $$
When the bike meets the scooter, $y=ax$, so $4y=4ax$.
Therefore
$$ \begin{eqnarray} 10ax - 6x - 20a + 20 &=& 4ax \\ 6ax - 6x &=& 20a - 20 \\ 3ax - 3x &=& 10a - 10 \\ 3x(a-1) &=& 10(a-1) \\ 3x &=& 10 \\ x &=& 3\frac{1}{3} \end{eqnarray} $$
Teachers' Resources
The notes for the problem Four on the Road give a suggested approach for this problem.
Use of graphing software or graphical calculators to draw graphs representing the given information can give a lot of insight into what changes and what stays the same when the freedoms of the problem are explored.
