Gold again
Without using a calculator, computer or tables find the exact values of cos36cos72 and also cos36 - cos72.
Problem
Image
|
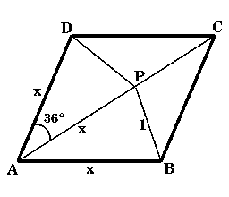
Consider the rhombus as illustrated where $x$ is an unknown
length, $AP = AD = x$ , angle $DAP = 36$ degrees and $P$ is a point
on the diagonal $AC$ such that $PB = 1$ unit.
Without using a calculator, computer or tables find the exact
values of
1. $\cos36^{\circ}\cos72^{\circ}$
2. $\cos36^{\circ} - \cos72^{\circ}.$
|
Image
|
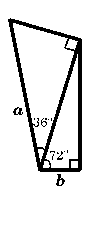
3. Draw these two diagrams as accurately as you can and measure the lengths $a$ and $b$. What do you notice? Can you prove it? (In each diagram there are two right angled triangles). | Image
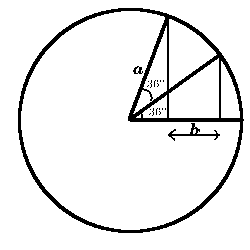
|
Getting Started
Find all the angles and lengths in the diagram. Use the cosine
rule.
Student Solutions
The first part of this solution came from Dorothy, S4, Madras College, St Andrew's and the second part from Vassil, Y11, Lawnswood High School, Leeds.
Consider the rhombus as illustrated, where $x$ is an unknown length. We have to find the value of $\cos 36^\circ \cos 72^\circ .$
I filled in the remaining angles and lengths, showing triangles $PCB$ and $PCD$ to be isosceles triangles with angles of $108^\circ$, $36^\circ$ and $36^\circ$ and sides $PC = PB = PD = 1$ unit.
Image
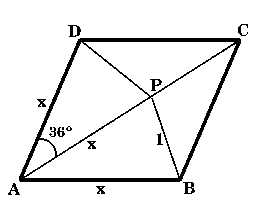
|
I found $\cos 36^\circ$ and $\cos 72 ^\circ$ by using the cosine rule for triangles DCP and APD respectively. \[ \cos 36^\circ = {{x^2 + 1 - 1}\over 2x} = {x\over 2} \] \[ \cos 72^\circ = {{1 +x^2 - x^2}\over 2x} = {1\over 2x} \] Combining these two expressions, \[\cos 36^\circ \cos 72^\circ = {x\over 2}.{1\over 2x}={1\over 4}.\] |
Consider the area of the triangle `above' the diagonal, and
express it is the sum of two areas : \[{1\over 2} x^2 \sin
108^\circ = {1\over 2} x\cdot1\cdot\sin 72^\circ + {1\over 2}
1\cdot 1\cdot\sin108^\circ.\] As $\sin 108^\circ = \sin 72^\circ$,
this gives $x^2=x+1$ and hence $x$ is the golden ratio: \[x =
{1+\sqrt{5}\over 2} = \varphi .\] Hence \[\cos 36^\circ - \cos
72^\circ = {x\over 2} - {1\over 2x} = {x^2-1\over 2x}={1\over
2}.\]
|
| Here we have ${{x + b}\over a} =\cos 36^\circ$ and ${x\over a} = \cos 72^\circ$ so \[{b\over a} = \cos 36^\circ -\cos 72^\circ = {1\over 2}.\] Therefore $a$ is twice the length of $b$. | Image
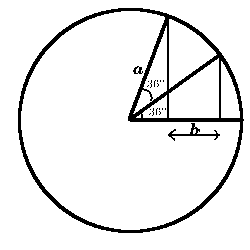
|
