Biggest Bendy

${\bf METHOD}$ ${\bf 1}$

First she applied Brahmagupta's formula for the area of a quadrilateral:

$ \delta = \sqrt{(s - a)(s - b)(s - c)(s - d) - abcd \cos^2 \beta}$

where $ s = \frac{1}{2}(a + b + c + d)$ and $\beta = \frac{1}{2}(A + C)$ or $ \frac{1}{2}(B + D)$.

Hence the area is clearly the greatest when $abcd \cos^2 \beta$ is least. Since $\cos^2 \beta$ is always positive, this value is least when $\beta $ is $90$ degrees as $\cos 90^{\circ} = 0$. Hence $\frac{1}{2}(A + C) = 90 $ and so $A + C = 180$ showing that the opposite angles in the quadrilateral add up to $180^{\circ}$ and so the area of a quadrilateral with fixed lengths of sides is greatest when it is cyclic.

This method gives a proof of the required result but you have to assume Brahmagupta's formula and Sue's second method uses only the formula for the area of a triangle.

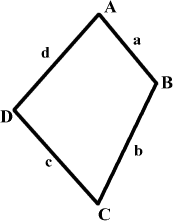
The area of the quadrilateral $ABCD$ can be expressed as the sum of the areas of triangle $ABD$ and $BCD$. Let the area of $ABCD$ be $\Delta$. Then \[ \Delta = \frac{1}{2} ad\sin A + \frac{1}{2} bc \sin C \] Thus $$\frac {d\Delta}{dA} = \frac{1}{2} ad\cos A + \frac{1}{2} bc \cos C \frac {dC}{dA}.\quad (1)$$

From the Cosine Rule, $$a^2 + d^2 - 2ad\cos A = b^2 + c^2 - 2bc\cos C,$$

Hence, (differentiating both sides with respect to $A$), $$2ad\sin A = 2bc\sin C \frac {dC}{dA}.\quad (2)$$

From (1) and (2), $$\eqalign{ \frac{d\Delta}{dA} = \frac{1}{2} ad\cos A + \frac{1}{2} bc \cos C{ad\sin A \over bc\sin C}\\ = \frac {ad\cos A \sin C + \sin A \cos C}{2\sin C}\\ = \left(\frac{ad}{2}\right) \frac{\sin (A + C)}{\sin C} }.$$ Hence, for the maximum area, $\sin (A + C)=0$ and $A+C=\pi$ which makes the quadrilateral cyclic.

We can show that this gives the maximum and not the minimum value of $\Delta$ by finding the second derivative.