Bendy quad
Four rods are hinged at their ends to form a convex quadrilateral. Investigate the different shapes that the quadrilateral can take. Be patient this problem may be slow to load.
Problem
Four rods are hinged at their ends to form a convex quadrilateral with sides of length $3$, $4$, $5$ and $6$ (in that order). Investigate the different shapes that the quadrilateral can take.
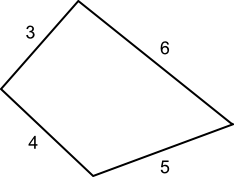
What are all the possible values of the angles if the quadrilateral is convex?
Getting Started
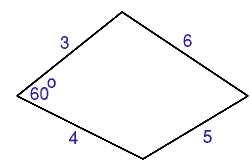
Suppose one angle is 60 degrees as shown in the diagram.
Suppose the angle $s$ is $60$ degrees, then it is easy to calculate the length of the diagonal and from that to calculatethe opposite angle in the diagram.
You might like to check your answer by drawing the quadrilateral accurately, using ruler and compasses only, and then measuring the angles.
Calculate the other angles of the quadrilateral.
Now calculate the angles of the cyclic quadrilateral formed by keeping the lengths of the sides the same and changing the angles so that opposite angles add up to 180 degrees. You might wish to use a spreadsheet.
Image
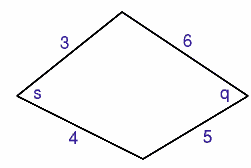
| The question states that the quadrilateral is convex; this means that the angles $s$ and $q$ are at most $180$ degrees.
Imagine moving the rods to make the angle $s$ as large or as small as possible. Find the largest and smallest values of $s$ and $q$. |
Student Solutions
The first thing some solvers did was to play with the interactivity to see what things they could change and what they couldn't.
Playing with the interactivity told us that if we change one thing, we can't change anything else without affecting the thing we changed first. For example, we moved point B to change the angle at A, and this then fixed the rest of the shape (when we tried to move C, the angle at A changed). We checked why this was the case by constructing the shape with ruler and compasses. If we picked a particular angle at A, there was only one possible quadrilateral with the correct lengths. We thought about this in terms of the two triangles ABD and BCD. This links to our work on congruent triangles.
We then started to investigate the shapes we could make.
The smallest that angle A can be is just above $0^{\circ}$ giving a long thin quadrilateral:
Angle C is also very close to $0^{\circ}$, and angles B and D are both very close to $180^{\circ}$.
Then we made angle A as big as we could. If it went over $180^{\circ}$ the quadrilateral would no longer be convex and if it was equal to $180^{\circ}$ we would have a triangle. This picture shows what the shape looks like when angle A is close to $180^{\circ}$
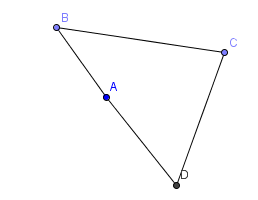
When angle A is $180^{\circ}$, angles B and D are as small as they can possibly be, and angle C is as large as it can possibly be. If we tried to make B and D smaller or make C bigger, A got bigger too.
We drew the shape as a triangle to help us to work out the minimum values of B and D, and the maximum value of C.
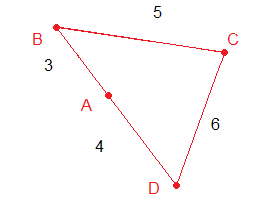
BCD is a triangle with sides $7$, $6$ and $5$ units.We used the Cosine Rule to work out angle B.
${CD}^2 = {BC}^2 +{BD}^2-2(BD)(CD)cosB$
$6^2=5^2+7^2-2 \times 5 \times 7 \times cosB$
We rearranged this to get
$$ cos B = 0.543$$
which gave $$B = 57.1^{\circ}$$
Then we worked out angles C and D in the same way.
Angle C is $78.5^{\circ}$ and angle D is $44.4^{\circ}$ (all our numbers have been rounded to $3$ significant figures).
| This shows that all the quadrilaterals will have angle A between 0 and 180, B between 57.1 and 180, C between 0 and 78.5 and D between 44.4 and 180. Can you find any special quadrilaterals with angles in these ranges? Are there any with right angles in? Any cyclic quadrilaterals? We would love to hear about anything interesting you discover! |
Teachers' Resources
Why do this problem?
This problem involves the interpretation of a very simple concrete structure, a linkage of 4 rods, and the angles that the quadrilateral formed by the rods could make if the joints between the rods at the vertices are totally flexible. Experimental evidence will offer ideas which then need justification and proof by forming convincing arguments.
The solution uses the cosine and sine rules. To find the constraints on the angles in the general case requires an argument using inequalities.
Possible approach
You might allow time for learners to explore the quadrilateral using strips of card or plastic and split pins, or a dynamic geometry package. This will help them to identify what can be varied and what not.
Discuss the freedoms and constraints within the problem, the impact these might have and how they could influence the structure of any investigation (what can be changed and what cannot).
Encourage groups to identify ideas that they would like to investigate. Spend time planning what they might do and sharing ideas before developing them.
Share findings and approaches.
Key questions
- What are your variables?
- If you flex the quadrilateral can the angles be any size?
- Can you find a relation between the cosines of opposite angles?
- What constraints would you like to impose? For example, that the quadrilateral is cyclic.
Possible support
Try the problem Diagonals for Area, also about bendy quads but only using the area of a triangle.
Possible extension
Try Biggest Bendy , Flexi Quads , Flexi Quad Tan
