Incircles
The incircles of 3, 4, 5 and of 5, 12, 13 right angled triangles
have radii 1 and 2 units respectively. What about triangles with an
inradius of 3, 4 or 5 or ...?
Problem
Image
|
(1) Show that the largest circle that fits inside a triangle
whose sides have lengths 3, 4, 5 has radius 1.
(2) Show that the largest circle that fits inside a triangle
whose sides have lengths 5, 12, 13 has radius 2.
(3) Can you find a right-angled triangle such that the largest
circle that fits inside it has radius 3? Of course, one such
triangle has sides of lengths 9,12,15 (which is obtained by scaling
the 3,4,5 triangle by a factor 3) but can you find another?
|
What about an inradius of 4 or 5 or ...?
Getting Started
Think about tangents to circles.
Student Solutions
Image
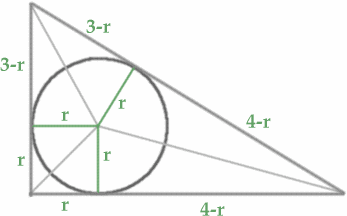
Ruoyi Sun, Sarah and Elizabeth from the North London Collegiate School Puzzle Club sent this neat solution.
"We found that by drawing the angle bisectors to find the centre of the incircle, and then drawing in 3 radii, we had created three pairs of congruent triangles. Therefore we found that part of the hypotenuse of the 3-4-5 triangle must have length $4-r$ and the other part $3-r$. We formed an equation $$3 - r + 4 -r = 5$$ hence $r = 1.$ For the 5-12-13 triangle the equivalent formula is $$5 - r + 12 - r = 13$$ and hence $r = 2.$"
Sue Liu of Madras College went further to find a formula for other Pythagorean triples for right angled triangles with incircles of radius $k$ for any integer $k$ and this is Sue's method.
"Clearly the largest circle that fits into a triangle is the incircle where the circle touches the three sides of the triangle. For a right angled triangle we can draw radii of length $r$ from the centre of the incircle perpendicular to each of the three sides $a$, $b$ and $c$. By equating areas we get $${1\over 2}ar +{1\over 2}br +{1\over 2}cr ={1\over 2}ab.$$ $$r = {ab\over a + b + c}.$$ For the 3-4-5 triangle $r = 12/(3 + 4 + 5) = 1$ so the incircle has radius 1. For the 5-12-13 triangle $r = 60/(5 + 12 + 13) = 2$ and the inradius is 2. The next part of the question asks us to find right angled triangles with incircle radius 3 and sides which are a primitive Pythagorean triples. Pythagorean triples ${a, b, c}$ are given parametrically by $$a = 2mn, \ b = m^2 - n^2, \ c = m^2 + n^2$$ where the integers $m$ and $n$ are coprime, one even and the other odd, and $m> n.$ We can consider a triangle with side lengths $2mn, \ m^2 - n^2, \ m^2 + n^2$ Again by equating areas as before, $${1\over 2} (2mnr + (m^2 - n^2)r + (m^2 + n^2)r) = {1\over 2}(m^2 - n^2)2mn$$ Hence $$r = {2mn(m^2 - n^2) \over 2m(m + n)} = n(m -n).$$ By taking $n=1$ and $m=k + 1$ or alternatively $n = k$ and $m = k + 1$ we get $r = k$ for any integer $k$ (and of course the triangle has inradius $k$ even when $k$ is not an integer). For $r = 3$ we have $n = 1$ and $m = 4$ giving the triangle with sides 8, 15 and 17 or alternatively $n =3$, $m = 4$ in which case $a = 24$, $b = 7$ and $c = 25$. For $r = 4$ we can take $n = 4$, $m = 5$ which gives the Pythagorean triple $a = 40$, $b = 9$ and $c = 41$."
Sue's generalisation of this problem to isosceles triangles is given as a Further Inspiration.
Teachers' Resources
Why do this problem?
The first two parts require only applying the idea that the tangents from an external point to a circle are equal and the radius is perpendicular to the tangent at the point of contact.
Possible approach
The first two parts could be tackled by the learners independently.
For the third part the formula for generating Pythagorean triples is needed.
Key questions
What facts do you know about tangents to circles?
What do you know about areas of triangles?
What is the formula for generating Pythagorean triples?
Possible support
Three articles: Pythagorean Triples I, Pythagorean Triples II and Picturing Pythagorean Triples.
Possible extension
The problem Pythagoras Mod 5
See the article Incircles which generalises this problem.
