You may also like

problem icon

Russian Cubes

How many different cubes can be painted with three blue faces and three red faces? A boy (using blue) and a girl (using red) paint the faces of a cube in turn so that the six faces are painted in order 'blue then red then blue then red then blue then red'. Having finished one cube, they begin to paint the next one. Prove that the girl can choose the faces she paints so as to make the second cube the same as the first.

problem icon

N000ughty Thoughts

Factorial one hundred (written 100!) has 24 noughts when written in full and that 1000! has 249 noughts? Convince yourself that the above is true. Perhaps your methodology will help you find the number of noughts in 10 000! and 100 000! or even 1 000 000!

problem icon

Euler's Officers

How many different solutions can you find to this problem? Arrange 25 officers, each having one of five different ranks a, b, c, d and e, and belonging to one of five different regiments p, q, r, s and t, in a square formation 5 by 5, so that each row and each file contains just one officer of each rank and just one from each regiment. There is an interactive version of this problem.

Doodles

Stage: 4 Challenge Level: Challenge Level:1
James cracked this toughnut for us:

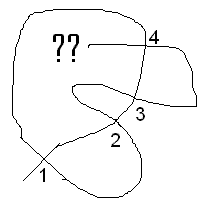
To prove that each vertex number in the list twice, I noticed to get back to where we started pointing in the same direction we started we must go fully around the curve. So we will cover the entire curve, and since the curve goes through each vertex twice, the number of each vertex will appear twice.

For the next part, I tried to doodle with an odd number of vertex number between the pair:
As expected, I ran into some problems. If we consider the number between the pair of 1's. Going around anti-clockwise 2 crosses, then 3, then 4, and so on. If there are an odd number of crosses then the end of the line will end up inside the loop. But it can't cross this line again, and so we will always have one end of the line stuck inside the loop, and one outside, and so the curve couldn't be closed.

So between every pair we must have an even number of vertex numbers (since any pair will form a loop similarly to above).

The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.