Sine and cosine for connected angles
Problem
The diagram shows a nine-point pegboard. We'll take the board radius as one (in other words it's a unit circle).
Looking at triangle $OAM$, why is $AM$ equal to $\sin40^\circ$?
Looking at triangle $OAB$, why is $AB$ equal to $2\sin20^\circ$?
Looking at triangle $ABM$, why is $AM$ also equal to $AB\cos20^\circ$ which works out as $2\sin20^\circ$ $\cos20^\circ$
So it looks like the same $AM$ length value can be calculated by using $\sin40^\circ$
and also calculated by using $2\sin20^\circ\cos 20^\circ$
Now switch to a $10$ point pegboard and find the two ways to calculate the $AM$ length on that board.
How about on a $12$ point board? What general result is emerging?
Draw a diagram and use it to provide reasoning which accounts for that general result.
For printable sets of circle templates for use with this activity, please see Printable Resources page.
Many thanks to Geoff Faux who introduced us to the merits of the 9 pin circular geo-board.
The boards, moulded in crystal clear ABS that can be used on an OHP (185 cm in diameter), together with a teacher's guide, are available from Geoff at Education Initiatives
Getting Started
Next use your knowledge of Sine or Cosine to find calculations for as many lengths as possible.
Remember this is a unit circle, the length $AO$ for example is $1$.
Student Solutions
Chris from Saint John Payne School sent in clear diagrams to explain the first part.
Diana thought about a general result. Here's what she sent us.
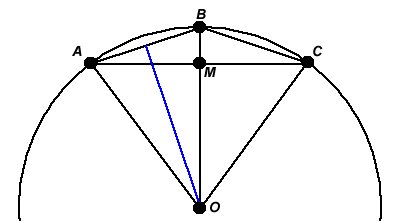
In general, suppose that we've placed points $A$, $B$ and $C$ in such a way that $\angle A O B=\angle B O C=2\theta$. I'm going to show that $\sin(2\theta)=2\sin\theta\cos\theta$. This is called a double angle formula.\par From triangle $O A M$, we know that $A M=\sin(2\theta)$ (as the circle has radius $1$).
From triangle $O A B$, we know that $A B=2\sin\theta$ (the blue line bisects the angle at $O$ and since triangle $A O B$ is isosceles, the blue line meets $A B$ at a right angle, so we can think about two right-angled triangles, each with angle $\theta$ at $O$).
Since $\angle A B O=90^{\circ}-\theta$ (from the isosceles triangle $A O B$), we know that $\angle B A M=\theta$, and so from triangle $A B M$ we see that $A M=A B\cos\theta$.
Putting together the last two paragraphs, we get $A M=2\sin\theta\cos\theta$. But also $A M=\sin(2\theta)$, so $\sin(2\theta)=2\sin\theta\cos\theta$.
Teachers' Resources
The pegboard gives a simple context in which to discover and explore this relationship.
