Nine-pin Triangles
How many different triangles can you make on a circular pegboard that has nine pegs?
Problem
You may like to use the interactivity to try out your ideas. Click on two of the dots to create a line between them.
If you prefer to work on paper, you might find this sheet of nine-peg boards useful.
Once you've had a go at this, why not investigate the number of different triangles you can create on circular pegboards with more or fewer pegs?
You might also like to have a look at this task for some extension questions!
Many thanks to Geoff Faux who introduced us to the merits of the nine-pin circular geoboard.
For further ideas about using geoboards in the classroom, please see Geoff's publications available through the Association of Teachers of Mathematics (search for 'geoboards').
Getting Started
How will you record the triangles you've made? You might like to print off this sheet to use.
You could try drawing triangles which have a side made by joining two pegs next to each other. How many different triangles can you make in this way?
How will you know when you've got them all?
Student Solutions
Cong who goes to St. Peter's RC Primary, Aberdeen, sent in a good solution to this problem. The key to answering it is to be sure you know what you mean by "different" triangles. Cong found 7 different triangles could be drawn on the nine-pin board which he drew:
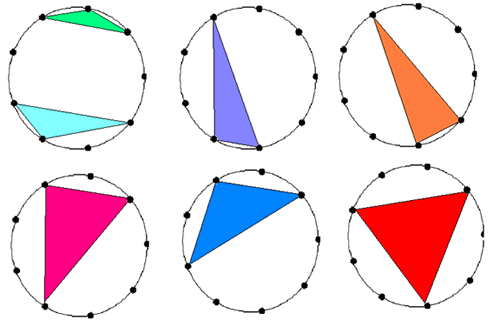
He also sent in a table which gave some more information about each triangle:
| Number | Colour | Type |
| 1 | Green | Isosceles |
| 2 | Light blue | Scalene |
| 3 | Purple | Scalene |
| 4 | Orange | Isosceles |
| 5 | Pink | Scalene |
| 6 | Blue | Isosceles |
| 7 | Red | Equilateral |
Richard, a teacher from Cliff Lane Primary School, sent in the following:
There are 28 triangles to be made.
My class started by drawing the triangles from one peg. There were 7 possible triangles connecting peg 1 and 2, keeping that first short line constant.
They then kept peg 1 the same and connected it to peg 3, keeping this constant. They were able to make triangles using pegs 4, 5, 6, 7, 8 and 9. This results in 6 possible triangles.
They repeated for a constant line from peg 1 to peg 4 and found 5 triangles. They recognised the following pattern:
Constant line
Peg 1 - 2 7 triangles
Peg 1 - 3. 6 triangles
Peg 1 - 4. 5 triangles
Peg 1 - 5. 4 triangles
Peg 1 - 6. 3 triangles
Peg 1 - 7. 2 triangles
Peg 1 - 8. 1 triangle
Peg 1 - 9. 0 triangles
They added these up and found 28 triangles. This could be repeated for each new peg, but the triangles would be repeated, so would not count in the final total.
The next two solutions looked at a way of getting all the triangles by getting a series of numbers connected to the 9 points.
This is a good idea, and, as so often happens in mathematics as well as helping, can produce a problem. So while 123,124,125,126,127,128,129, as a starting point is a good idea the problem arises when you go to ones starting with 234,235,236,237,238,239 it looks like we have made a further six but the size and shape of 123 is identical to 234. The same is true for the ones that would follow on. It's a matter of not losing sight of what the numbers are representing.
The next solutions did well to see that 123,321,213,312,231,132 are all the same.
Here is Tiffany's, then Claire's, work from Citipointe Christian College in Australia:


- - - - - -


Jiwoo and Sushi then Harry, Judy and Mai from The British International School Ho Chi Minh City in Vietnam sent these in:


Thank you for these excellent thoughts and conclusions about this task, we hope to see you send in more solutions in the future.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
