Triangle Pin-down
Problem
A right-angled triangle has been drawn on the four-pin board above left.
Can you draw the same type of triangle on a three-pin board?
How many pins could there be on the board for you to be able to draw the same type of triangle?
Do you notice anything about the number of pins for which this is possible?
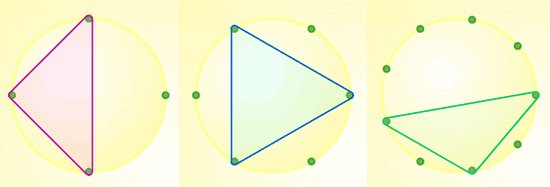
What kind of triangle is drawn on the six-pin board above?
How many pins could there be on the board for you to be able to draw the same type of triangle?
Do you notice anything about the number of pins for which this is possible?
Can you name the type of triangle drawn on the nine-pin board above?
On what size board could you draw the same type of triangle?
Do you notice anything about the number of pins for which this is possible?
You might like to use the interactivity to try out your ideas.
Once you have chosen the number of dots you need, select the line drawing tool. Click on two points to draw a line between them.
For printable sets of circle templates for use with this activity, please see Printable Resources page.
Many thanks to Geoff Faux who introduced us to the merits of the 9 pin circular geoboard.
For further ideas about using geoboards in the classroom, please see Geoff's publications available through the Association of Teachers of Mathematics (search for 'geoboards').
Getting Started
How will you record the triangles you can make? You might like to print off these sheets if you're not using the interactivity:
Sheet of three-peg boards
Sheet of four-peg boards
Sheet of five-peg boards
Sheet of six-peg boards
Sheet of seven-peg boards
Sheet of eight-peg boards
Sheet of nine-peg boards
Student Solutions
If you interpret "same type of triangle" to mean any right-angled triangle, your answer would be different. What would it be?
Bob has an answer for the six-pin board :
Can you give an explanation for these observations?
Thank you to Kyle from New Zealand who correctly identified certain circles and states the type of triangle as
If you consider that an isosceles triangle can also be a right-angled triangle, then many answers are possible. Do you think that we can consider an equilateral triangle to be a special form of isosceles triangle?
Teachers' Resources
Why use this activity?
This activity encourages children to explore the angles and relative lengths of sides of different triangles that can be made on pinboards. All the angles can be worked out using angles at the centre of a circle and the fact that the three angles in a triangle sum to $180^{\circ}$. No more complex geometric knowledge is required.
It might help for learners to have copies of blank peg boards to record their work on. These can be downloaded here:
Sheet of three-peg boards
Sheet of four-peg boards
Sheet of five-peg boards
Sheet of six-peg boards
Sheet of seven-peg boards
Sheet of eight-peg boards
Sheet of nine-peg boards
Teachers may find the article Angle Measurement: An Opportunity for Equity to be of interest.
Possible approach
The task can be introduced to the whole class using an interactive whiteboard and involving the children in contributing to decisions about their answers.
The children could then try the task for themselves either on computers or using the sheets of geoboard pictures. Once they have had a chance to explore, support them in feeding back their solutions to the rest of the class. Different groups might work on different numbers of pegs.
Key questions
The key questions are given in the text of the problem but here they are again:
Can you draw the same type of triangle on a three-pin board?
How many pins could there be on the board for you to be able to draw the same type of triangle?
Do you notice anything about the number of pins for which this is possible?
What kind of triangle is drawn on the six-pin board?
How many pins could there be on the board for you to be able to draw the same type of triangle?
Do you notice anything about the number of pins for which this is possible?
Can you name the type of triangle drawn on the nine-pin board?
On what size board could you draw the same type of triangle?
Do you notice anything about the number of pins for which this is possible?
Possible extension
You could extend the problem to pinboards with more pins on them and learners could explore the relationship between the number of pins, the shapes and angles involved.
Possible support
Children will find this easier if they have the opportunity to engage with the task on real pinboards. They may also find it difficult to record their results. Encorange them to draw or mark the lines from the centre to the edge of the triangles.
