Old Nuts
Problem
Four people are shipwrecked and there are only coconuts to eat. Being prudent they collect all the coconuts they can find and weary from their work fall asleep.
In the night one of the castaways wakes up and secretly divides the coconuts into four equal piles, she hides her share and throws to the monkeys the three that were left over before putting all the remaining nuts back into one pile.
Later another of the castaways wakes up and she too secretly divides the coconuts into four equal piles, she hides her share and throws to the monkeys the three that were left over before putting all the remaining nuts back into one pile.
Later still, yet another of the castaways wakes up and she too secretly divides the coconuts into four equal piles, hides her share and throws to the monkeys the three that were left over before putting all the remaining nuts back into one pile.
Just before morning the last castaway wakes up and she too secretly divides the coconuts into four equal piles, hides her share and throws to the monkeys the three that were left over before putting all the remaining nuts back into one pile.
Next morning with a much reduced pile the four castaways find they can share out equally all the coconuts that are left!
What is the least number of coconuts they could have started with?
Extension: Solve the generalised problem with n castaways, dividing the pile into n shares, hiding one share and throwing m coconuts to the monkeys each time.
Getting Started
This can be solved by just working systematically with the information, thinking about which numbers are divisible by 4 and 3, and testing the possibilities.
Modulus arithmetic also provides an efficient way to solve the problem.
Student Solutions
Super solutions to 'Old Nuts' came in from Vassil Vassilev of Lawnswood High School, Leeds, Hyeyoun Chung of St Paul' Girls's School London and Elizabeth Whitmore of Madras College, St Andrew's.
Here is Vassil's diagram and Hyeyoun's solution:.
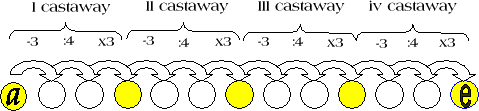
Let us call the total number of coconuts in the beginning $a$, then the number of coconuts in the remaining pile $b$, then the number of nuts in the next pile of remaining nuts $c$, and so on, the number of nuts in the last pile being $e$.
First of all we can say that: $a - 3$ is a multiple of 4.
We can also say that:
$b = 3(a -3 )/4$
$c = 3(b -3 )/4$
$d = 3(c -3 )/4$
$e = 3(d -3 )/4$
Then, as each pile has 3 nuts taken away from it and then is divided into 4 equal piles, we can say that:
$a - 3$ is a multiple of 4
$b - 3$ is a multiple of 4
$c - 3$ is a multiple of 4
$d - 3$ is a multiple of 4
Also, as each pile except for $a$ has been created by taking 3/4 of the previous pile minus 3, we can also say that:
$b$ is a multiple of 3 and $b - 3$ is a multiple of 4 and 3
$c$ is a multiple of 3 and $c - 3$ is a multiple of 4 and 3
$d$ is a multiple of 3 and $d - 3$ is a multiple of 4 and 3
$e$ is a multiple of 4 and 3, as the castaways were able to divide it exactly into four equal piles.
The least number of coconuts the castaways could have ended with will also give you the least number of coconuts they could have started with. The number of coconuts the castaways ended up with, $e$, is a common multiple of 4 and 3, which means it is a multiple of 12. The smallest common multiples of 4 and 3 are 12, 24, 36, 48, 60, 72, ...
Trying out these numbers one by one, the smallest multiple of 12 which satisfies the above conditions is 72. This is shown below:
When $e = 12$, $d = 4e/3+ 3 = 19$. However $d$ needs to be a multiple of 3 and so this will not work.
When $e = 24$, $d = 4e/3+ 3 = 35$. Again, this will not work.
When $e = 36$, $d = 4e/3+ 3 = 51$. This seems to work. However: see what follows.
When $d = 51$, $c = 4d/3+ 3 = 71$. As $c$ also needs to be a multiple of 3, this will not work either.
The same thing occurred with all the other multiples of 12. However, with 72:
When $e = 72$, $d = (4\times 72)/3 + 3 = 99$.
When $d = 99$, $c = 4d/3 + 3 = 135$.
When $c = 135$, $b = 4c/3 + 3 = 183$.
When $b = 183$, $a = 4d/3 + 3 = 247$.
Here, $b$, $c$, and $d$ are all multiples of 3, and $b - 3$, $c - 3$, and $d - 3$ are all multiples of 3 and 4. As $a$ does not have to be a multiple of either 3 or 4, this works.
Therefore, the least number of coconuts the castaways could have started with is 247.
You may like to apply the methods of modulus arithmetic and send in a Further Inspiration on this problem. See the NRICH articles on modulus arithmetic.
