More Total Totality
Is it possible to arrange the numbers 1-6 on the nodes of this diagram, so that all the sums between numbers on adjacent nodes are different?
Problem
This problem follows on from Total Totality.
This network has nine edges which meet at six nodes. The numbers $1, 2, 3, 4, 5, 6$ are placed at the nodes, with a different number at each node. Is it possible to do this so that the sum of the two numbers at the ends of an edge is different for each edge?
Image
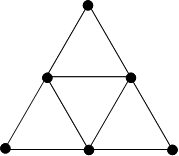
Either show a way of doing this, or prove that it is impossible.
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
It is not possible. In proving this, we call the sum of the two
numbers at the ends of an edge the 'weight' of that edge. Note that
three of the nodes are connected to exactly two nodes, while the
other three are connected to exactly four nodes. Thus the total of
the nine weights must always be an even number, whichever numbers
are placed at the nodes.
Now the smallest possible weight is $1+2=3$ while the largest
possible weight is $5+6=11$. As there are exactly nine edges, we
deduce that for the weights for each edge to be different they must
take the values $3, 4, 5, 6, 7, 8, 9, 10$ and $11$. However, the
total of these is $63$, an odd number, so the task is
impossible.
