Primary proof?
Many people would suggest that proof has no place in primary mathematics classrooms. It needs to be too formal and rigorous, and young children find it difficult to follow and even harder to replicate for themselves. We would disagree and suggest that, on the contrary, ideas of proof need to be introduced to children when they are quite young so that they become comfortable with one of the central ideas in mathematics.
John Mason (1982) suggests that central to ideas of proof are notions of conviction and he suggests that there are three levels of this. Firstly we can consider whether we are convinced ourselves, secondly we can try to convince a friend and, the most rigorous level, we can try to convince an 'enemy'. This means that the argument should be strong enough to convince someone who is sceptical and can dispute any slightly under-justified steps in it. If these ideas are mentioned to children at quite a young age, we find that they are responsive to them and start to internalise them and to use them independently on their own initiative when they are engaged in reasoning about a mathematical problem.
We have already mentioned several aspects of proof in the previous paragraph. In their book Primary Questions and Prompts for Mathematical Thinking, the authors (2004) suggest that generalising, justifying and convincing are key elements of mathematical thinking and my own research (Back, 2004) suggests that classrooms in which teachers encourage pupils to participate in mathematical reasoning and argument are more likely to be successful in helping children to be enthusiastic mathematicians.
Many of the problems that we offer here on the NRICH website focus on looking for general rules by looking at a number of particular cases. Although this activity does not involve creating proofs as such, it is an important part of the process of proof. The theme of the June 2005 website is proof and we are offering several problems of this type.
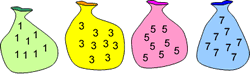
It hinges on what happens when you add two odd numbers. The proof would involve demonstrating that two odd numbers added together always give an even answer. What would we find acceptable as a proof at Key Stage 2 level? Here is one of the solutions that we put up on the website:
This is not the kind of proof one would expect from an adult or 'A' Level student but demonstrates a clearly reasoned and intelligible argument that convinces us certainly. In a recent article in 'Mathematics Teaching', Alf Coles (2005) talks about proofs that fail to convince even when one has followed every step of the logical path. He suggests that we need to offer children opportunities to gain insights into the mathematical contexts surrounding the proof before we can expect them to gain a thorough understanding and ownership of the proof itself. We would like to suggest that by offering children the opportunity to produce convincing arguments in writing or speech like the one above we will familiarise them with the process of creating proof so that the shifts to more formal expressions of proofs will come more easily later.
Several kinds of mathematical proof seem to be appropriate for introduction to young children. Possibly simplest is proof by exhaustion - only we have to be careful to choose problems that won't generate data that proves too exhausting! An example of this that we think works is the problem Crossings from the June 2005 website.

Hopefully the experience of dealing with something that is initially straightforward will lead children into offering us a proof that makes sense to them and will convince us.
We look forward to receiving your children's proofs on the website.
References:
Coles, A. (2005). Proof and Insight. Mathematics Teaching 190, Derby, ATM.
This article also appears in Primary Mathematics, a journal published by The Mathematical Association .
