Great Squares

Investigate how this pattern of squares continues. You could measure lengths, areas and angles.

Watch the Clock

During the third hour after midnight the hands on a clock point in the same direction (so one hand is over the top of the other). At what time, to the nearest second, does this happen?

Walk and Ride

How far have these students walked by the time the teacher's car reaches them after their bus broke down?

Chippy's Journeys

Age 7 to 11
Challenge Level

We received lots of correct answers to the first part of this problem but very few of you told us how you went about solving it. Some of you drew a diagram of Chippy's route, which was a very good way of tackling it. Rukmini from Hopscotch Nursery and Christy, sent particularly clear pictures. Here is Rukmini's:

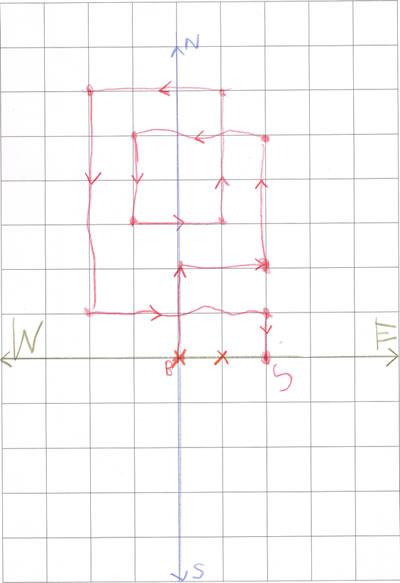
Rukmini says:

First I took some checked paper and drew a map showing North, East, West and South. In the centre was the Base station which I marked as B on the map. From B, I counted squares Chippy went along. He seemed to go a bit round and round till he forgot where the basic station was. I marked with a 'S' where he stopped. I drew his way back with crosses. He needed to go $2$ m West to get back to the Base station.

Tom who lives in New Zealand, solved the the first part of problem in a different, but equally as good way. Here is what Tom says:

This is a table showing how many metres Chippy went:

	N	S	E	W
	2	2	2	3
	3	5	2	3
	3	1	4
Total	8	8	8	6

The north and the south amounts were the same so there was no change there, but the east and the west amounts were different. The east was $2$ metres more than the west. So you have to go $2$ metres in west at the end to get to Chippy's station.

Well done to you all for your well explained solutions.

You may also like

Great Squares

Watch the Clock

Walk and Ride

Chippy's Journeys

Age 7 to 11Challenge Level

Age 7 to 11
Challenge Level