Pentagonal
Can you prove that the sum of the distances of any point inside a
square from its sides is always equal (half the perimeter)? Can you
prove it to be true for a rectangle or a hexagon?
Problem
Image

Can you prove that the sum of the distances of any point inside a square from its sides is always equal?
Can you prove it to be true for a rectangle or a regular hexagon?
Does the hexagon need to be regular?
Can you show the same is the case for a regular pentagon?
Does the pentagon need to be regular?
Getting Started
If you have decided that the result holds for a regular hexagon, what is it exactly about the hexagon that lets it work?
What does a regular hexagon also have that isn't needed for this result?
For the regular pentagon, put a point somewhere inside, perhaps not at the centre.
Join that point to each of the vertices of the pentagon and think about the five triangles.
Finally, what does a regular pentagon also have that isn't needed for this result?
Student Solutions
Laura sent us her work on this problem. Well done, Laura!
Image

Let the square have side length $l$. Then its perimeter is $4l$. Also, we can see from the diagram above that the sum of the distances from the point to the top and bottom sides is $l$, and similarly the sum of the distances from the point to the left and right sides is $l$, so the total sum of the distances is $2l=\frac{1}{2}\times 4l$, which is constant and half of the perimeter.
Image
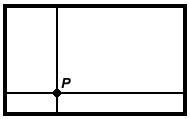
Let the rectangle have height $h$ and width $w$. Then its perimeter is $2(h+w)$. This is very similar to the square. Here the sum of the distances from $P$ to the top and bottom sides is $h$, and the sum of the distances from $P$ to the right and left sides is $w$, so the total sum of the distances is $h+w=\frac{1}{2}\times 2(h+w)$ is constant, and again is half of
the perimeter.
Image
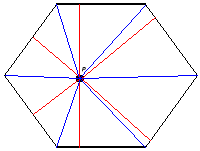
This hexagon isn't regular, but it is equilateral (all its sides have the same length, $l$, say). I've drawn on the perpendicular lines (in red) from $P$ to the sides, and have also divided the hexagon into six triangles (in blue), each with base $l$ and height the distance from that side to the point. The area of the hexagon can therefore be written as
$\frac{1}{2}(\textrm{sum of the heights})\times l$. Since this is constant, so is the sum of the heights.\par In the same way, the sum of the distances in an equilateral pentagon is constant.
Teachers' Resources
This problem offers opportunities to think about the properties of regular shapes and decide which do, and which do not, affect the result.
There is also opportunity for geometric reasoning based on area, but saying any more about that would give away too much about one route through the problem !
