Triangles within pentagons
Show that all pentagonal numbers are one third of a triangular number.
Problem
Image
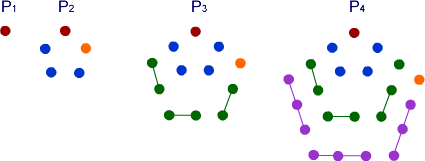
The diagram above shows the pentagon growing in a systematic
way to produce the pentagonal numbers. The equations below describe
this growth:
$$\begin{eqnarray} P_2 &=&
P_1 + 4 \\ &=&1+4 \\ &=&1 + 3 \times 1 + 1\\
P_3&=& P_2 + 7 \\ &=& 1+4+7 \\ &=& 1 + (3
\times 1 + 1) + (3 \times 2 + 1) \\ P_4 &=& P_3 + 10 \\
&=& 1 + (3 \times 1 + 1) + (3 \times 2 + 1) + (3 \times 3 +
1) \\ \end{eqnarray}$$
Can you find a general rule for $P_n$?
By writing a formula for the nth triangular number $T_n$, show
that all pentagonal numbers are one third of a triangular number
and prove that the triangular numbers involved are all of the form
$T_{3n-1}$
Getting Started
The diagram shows the groupings of the numbers which is mirrored in the derivation of the formulae.
The rule is generalisable but can you convince us why?
For the last part you need a formula for triangular numbers. Each triangular number is the sum of all the whole numbers so the fifth triangular number is 1+2+3+4+5.
By reversing and adding any group of consecutive numbers to itself you can generate the triangular numbers. The thesuarus might help here.
You might find it helpful to visualise the pentagonal numbers as made from triangular numbers.
Now you should notice that the formula for the pentagon numbers can be written in terms of triangular numbers.
There is a little bit of agebraic substitution necessary to get you to the point where you can show that every pentagonal number is a third of a triangular number.
Is the inverse the case?
Student Solutions
Curt from Reigate College started by getting a general formula for Triangle numbers
$T_n = 1 + 2 + 3+ . . . +(n-1) + n$
$T_n = n + (n-1) + . . . + 3+2+1$
The second line is just a repeat of the first but with the terms in reverse order.
Then adding the two lines the right hand side becomes $n$ lots of $n+1$
So $2T_n=n(n+1)$ and since everything was added in twice,
$T_n=\frac{n(n+1)}{2}$.
David from Sha Tin College used a known general result for any progression that steps up by a fixed amount term on term
$\frac{n}{2}(2a+(n-1)d)$
where n is the number of terms, a is the starting term and d is that step up.
If the step up is equal to 1, and the start value is also 1, you can see that this is the same result as Curt demonstrated.
Continuing with the Pentagonal numbers
The diagram shows $P_4=3T_3+4$
Image
And in general $P_n=3T_{n-1}+n$
Now using the result for $T_n$ to see $P_n$ in terms of $n$
$P_n=\frac{3n(n-1)}{2}+n$
We now have to show that three times that result is a triangle number
$3P_n=3[\frac{3n(n-1)+2n}{2}]$ and is the same as $3[\frac{3n^2-n}{2}]$
or
$\frac{3n(3n-1)}{2}$
And that's the same as $T_{3n-1}$ the required result.
Teachers' Resources
Having identified the rule is it possible to work backwards and reconstruct pentagons using the triangular numbers?
This problem builds on the work of the three problems "sequences and series ", "triangles within triangles " and "triangles within squares ".
There are many more patterns and relationships involving triangular numbers and some experimentation could result in some pupil generated discoveries.
