Triangles Within Squares
Can you find a rule which relates triangular numbers to square numbers?
Problem
Image
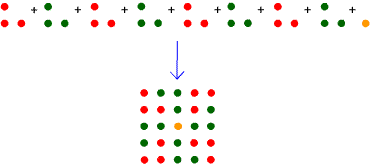
The diagram above shows that: $$ 8 \times T_2 + 1 = 25 = 5^2$$
Use a similar method to help you verify that: $$ 8 \times T_3 + 1 = 49 = 7^2$$ Can you generalise this result?
Can you find a rule in terms of $ T_n $ and a related square number?
Can you find a similar rule involving square numbers for $T_{n}, T_{n+2}$ and several copies of $T_{n+1}$?
Getting Started
There is a very strong connection between this problem and the "Sequences and Series" problem.
Can you see the rectangles made from two triangular numbers in the square?
Can you explain why there is always one left over?
Can you see the rectangles made from two triangular numbers in the square?
Can you explain why there is always one left over?
Student Solutions
Well explained by Tom, from Cottenham
Village College
The answer I got for $T_n$ is: $8T_n+1=(2n+1)^2$
The $2n+1$ part is because the diagram looks like this for
$T_3$
Image
$2T_n$ form a rectangle $n$ by $n+1$
The four rectangles rotate around the centre and together make
a square of side $n+(n+1)$
So we get the equation $8T_n+1=(2n+1)^2$
Teachers' Resources
Why not encourage pupils to discover rules of their own?
This problem links to "Triangles withinTriangles " and the problem "Triangles within Pentagons"
There are many different ways to visualise this question and pupils should be encouraged to explain how they "know" their rule works.
This problem links to "Triangles withinTriangles " and the problem "Triangles within Pentagons"
There are many different ways to visualise this question and pupils should be encouraged to explain how they "know" their rule works.
