Triangles within triangles
Can you find a rule which connects consecutive triangular numbers?
Problem
This diagram shows how the first
triangular number can be added to 3 copies of the second triangular
number to make the fourth triangular number:
Image
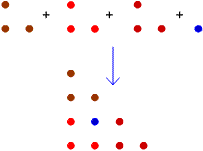
That is: $$ T_1 + 3 \times T_2 = T_4 $$ Here is a diagram showing how the second and third triangular numbers can be combined to make the sixth triangular number:
Image
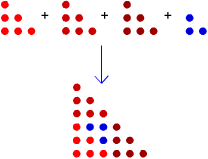
$$ T_2 + 3 \times T_3 = T_6 $$ Can you generalise this rule?
Can you find a rule in terms of $ T_n $ and $T_{n+1}$?
Getting Started
It is usefult to be able to recreate these patterns on square dotty paper.
Is the way the triangles fit together always going to work with two consecutive triangular numbers?
Why?
Yuu might find it useful to look at the problem on "Sequences and Series".
Is the way the triangles fit together always going to work with two consecutive triangular numbers?
Why?
Yuu might find it useful to look at the problem on "Sequences and Series".
Student Solutions
Well done Tom, from Finham Park School, for clear use of notation :
Whenever you add 3 triangles ( as in $T_2$ ) together with a triangle one size smaller ( as in $T_1$ ), a new triangle is formed ( $T_4$ ) , twice the height of the triangle which was used three times ( $T_2$ ) .
The smaller triangle can be called $T_n$ , while the 3 triangles one size up can be called $T_{n+1}$.
One of the $T_{n+1 }$ joins with the $T_n $ to form a square of side length $n+1$ .
The two remaining $T_{n+1}$ fit to that square producing a large triangle that has a height twice that of $T_{n+1}$ ,
So the sum of all four triangles is the triangle $T_{2(n+1)}$
So $T_n $ + $3T_{n+1} =T_{2(n+1)}$ or, if you prefer, $T_{2n+2}$
Teachers' Resources
Why not encourage pupils to discover rules of their own?
By using isometric paper the triangular numbers can be represented as equilateral triangles wich give scope to investigating their connection with hexagonal numbers.
This problem links to "Triangles within Squares ".
