Function Machines
Problem
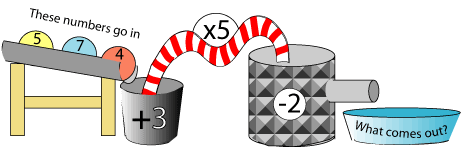
This one is a bit more of a puzzle.
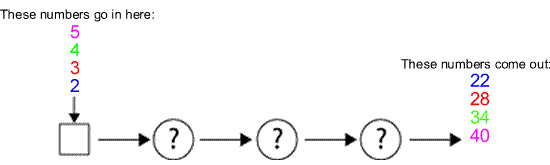
Can you work out what happens in the three circles?
Getting Started
You might like to start with $5$. Follow the operations in order - add $3$, multiply by $5$, take away $2$. What comes out?
How could you get from $2$ to $22$ ? Will those same operations turn $3$ into $28$?
Student Solutions
Well done to all of you who gave a correct solution to this problem. The correct answer to the first part of the question is $33, 48, 38$.
There are several correct answers to the second part of the problem including:
Richard from Burlingame School used a systematic approach to help him find the answer to the second part of the problem:
What I did was multiply each number by $2$, then $3$, then $4$, etc till I found a pattern. If you multiply the number by $6$, you come out with a number $10$ less than the answer. I simply added ten, then subtracted $0$ to give me the answer.
Quite a few of you used a really useful technique to help find the solution more efficiently including Marley and Jake from Swarcliffe Primary and Shiv from Mayplace Primary School. Ester sent in a nice solution:
The numbers are CONSECUTIVE going in and HAVE A DIFFERENCE OF $6$ coming out. This tells us that there must be a multiplication by $6$ somewhere.
She also spotted that there was more than one solution:
If $\times 6$ is in the middle circle some solutions could be
$+2, \times 6, -2$
$+1, \times 6, +4$
$-1, \times 6, +16$
If you multiply by six first you have to add or subtract in the last two circles so that the result is $+10$
$\times ,+6,+4$
$\times 6,+11,-1$
You cannot make the $\times 6$ the last thing you do because the numbers coming out are not in the six times table.
As you can see, there are lots of possible solutions using multiply by $6$ as one of the functions, but you can also split multiplying by $6$ into multiplying by $3$ and multiplying by $2$, or as several pupils from the Mount School in York observed, multiplying by $12$ and dividing by $2$.
