Octa-flower
Join some regular octahedra, face touching face and one vertex of
each meeting at a point. How many octahedra can you fit around this
point?
Problem
Image
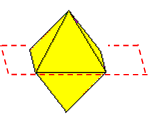
Start with a thought experiment in which you take some regular octahedra and, on each one, colour two faces that meet at a vertex but not along an edge. Now imagine taking two octahedra and gluing them together with coloured faces in contact so that the vertices where the coloured faces meet coincide. Now glue another octahedron on, coloured face to coloured face, so that the three vertices where the coloured faces meet coincide. Continue in the same way as long as possible. Calculate how many octahedra can be joined together in this way.
Getting Started
Think about a plane of symmetry.
Student Solutions
Think in 3D of a flower made from regular octahedra with the vertices of the octahedra meeting at a point and faces in contact. How many octahedra can be joined together in this way around one centre?
Here is a solution from Andrei of Tudor Vianu National College, Bucharest, Romania.
First, I observe that the octahedron is symmetrical about a plane that passes through the 4 coplanar vertices (see figure), so for the problem I may take into account only a pyramid.
Image
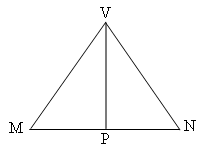
I shall calculate angle $MVN$.
Image
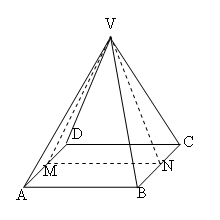
As all exterior sides have equal lengths, without loss of generality I may assume $AB = 1$. In this case $VN$ is the height of equilateral triangle $VBC$, so it has a length of $\sqrt 3 /2$. $MN$ is equal to $AB$, having a length of 1.
To calculate angle $MVN$, I shall calculate its sine.
Image
$$\eqalign { \sin MVN &= 2\sin{{\angle MVN \over
2}}\cos{{\angle MVN \over 2}} \cr &= 2{MP\over MV}{VP\over
MV}\cr &= 2. {1/2 \over \sqrt 3/2}.{\sqrt 2/2 \over \sqrt
3/2}\cr &= {2\sqrt 2 \over 3} }$$
The angle at $MVN$ (to 3 decimal places) is $$\sin^{-1}2\sqrt
2/3 = 70.529^o .$$ Alternatively you could calculate this angle as
$$2\sin^{-1}1/\sqrt 3 = 70.529^o .$$ The number of octahedra is
$360/70.529 = 5.1$.
So 5 tetrahedra could be joined together in this way.
Teachers' Resources
You need to know that a regular octahedron has eight faces, each of which is an equilateral triangle and that four of the triangles meet at each vertex.
