Golden construction
Draw a square and an arc of a circle and construct the Golden
rectangle. Find the value of the Golden Ratio.
Problem
In this problem you start with a square, construct a golden rectangle and calculate the value of the golden ratio.
When you cut a square off a golden rectangle you are left with another rectangle whose sides are in the same ratio. In the diagram below, if you remove the orange square from rectangle $AEFD$, you are left with the yellow rectangle whose sides are in the same ratio as $AEFD$.
Image
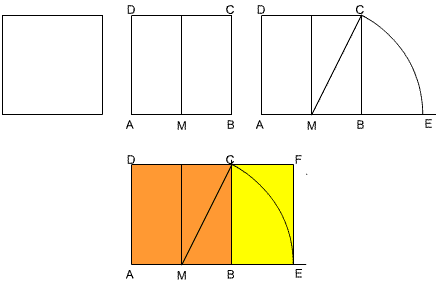
(1) Follow the instructions for drawing the rectangle $AEFD$. You can make the most accurate drawing by using a ruler and compasses. Draw a square $ABCD$ of side length 10 cm. Bisect $AB$ at $M$ and draw an arc of radius $MC$ to meet $AB$ produced at $E$. If you prefer you can just measure $MC$ and mark $E$ on $AB$ so that $ME=MC$. Draw $EF$ perpendicular to $AB$ to meet $DC$ produced at $F$.
Measure $AE$ and $BE$. From your measurements calculate the ratios $AE$/$AD$ and $BC/BE$. What do you notice?
(2) Calculate the exact lengths of $MC$, $AE$ and $BE$. Calculate the exact value of the ratios $AE$/$AD$ and $BC$/$BE$ and prove that they are equal. [Note: To get exact values you must work with surds and you will not be able to use a calculator.]
(3) Suppose this ratio is denoted by $\phi$ and take 10 cm as 1 unit then $AE$ is $\phi$ units. Show that $BE$ is $1/\phi$ units and hence $$\phi = 1 + {1\over \phi}\quad (1)$$
Explain just from equation (1), and without solving the equation, why the equation must have a solution between 1 and 2.
(4) Draw the graphs of $y=x$, $y=1/x$ and $y=1+1/x$ on the same axes and use your graph to find an approximate value for $\phi$.
(5) Solve equation (1) to find the value of $\phi$.
Getting Started
Just do part 1 if you like where you will construct a golden rectangle and find an approximate value of the golden ratio by measurement.
If you want to go further there are many hints within this question to take you through it. You will find the value of $\phi$ first by drawing and measurement, then by using geometry and calculating with surds (square roots), then by taking a reading from a graph and finally by rearranging a formula into a quadratic equation and solving it.
Student Solutions
Image
Thank you to Shaun from Nottingham High School and Andrei from Tudor Vianu National College, Bucharest, Romania for these solutions.
(1) Drawing the figure, I observe that ratios $AE/AD$ and $BC/BE$ are approximately equal, having a value of 1.6.
(2) From Pythagoras' Theorem I calculate $MC$ (in the right-angled triangle $MBC$): $$\eqalign{ MC^2 &= BC^2 + MB^2 = 1 + 1/4 \cr MC &= \sqrt5 /2 }.$$ So $AE=(\sqrt 5 + 1)/2$ and $BE=(\sqrt 5 - 1)/2$. The ratios are: $${AE\over AD}= {\sqrt 5 + 1\over 2}$$ and $${BC\over BE}= {1\over (\sqrt 5 - 1)/2} = {\sqrt 5 + 1\over 2}.$$ So, $AE/AD = BC/BE.$
(3) From this equality of ratios, I find out that $$BE = {AD.BC\over AE} = {1\over \phi}$$ But $AE = AB + BE$ so $$\phi = 1 + {1\over \phi}.$$
Image
(4) Substituting $\phi = 1$ the left hand side of this expression is less than the right hand side. If we increase the value given to $\phi$ the left hand side increases and the right hand side decreases continuously. Substituting $\phi = 2$ the left hand side is greater than the right hand side so the value of $\phi$ which satisfies this equation must lie between $1$ and $2$.
The two solutions of the equation can be found at the intersection of the cyan curve ($y=1 + 1/x$) and magenta curve ($y=x)$. Only the positive value is considered and it is approximately 1.618.
(5) Now, I solve the equation. It is equivalent to $\phi^2 - \phi -1 = 0$ so the solutions are $$\phi_1 = {1-\sqrt 5\over 2}$$ and $$\phi_1 = {1+\sqrt 5 \over 2}.$$ Only the second solution is valid because $\phi > 0$ .
Teachers' Resources
Once you have done the construction the different parts of this investigation can be taken separately and there is no need to tackle every part.
The problem solver is led through several different ways of finding the value of the Golden Ratio $\phi$ and proving that the various relationships are equivalent.
Younger problem solvers can simply stop at measuring the lengths and finding that the ratio of the sides of the rectangle $AEFD$ is the same as the ratio of the sides of the smaller rectangle $CBEF$ you get by removing a square from $AEFD$. This shows that $AEFD$ and $CBEF$ are golden rectangles.
You need Pythagoras' theorem and to be able to work with surds to get an exact value of this ratio in terms of $\sqrt 5$.
Alternatively, if you call this ratio $\phi$, then you can deduce that $$\phi = 1 + {1\over \phi}$$ and use a graphical method to solve this equation.
Lastly, if you know about quadratic equations, you can solve the quadratic equation to find the value of $\phi$.
