Cyclic Triangles
Make and prove a conjecture about the cyclic quadrilateral
inscribed in a circle of radius r that has the maximum perimeter and the maximum area.
Problem
Image

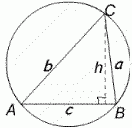
A triangle $ABC$ is inscribed in a circle with $AB$ as diameter. Find the maximum value of $AC + CB$.
Now generalise your result to the case where $AB$ is fixed but not a diameter of the circle.
Make and prove a conjecture about the cyclic quadrilateral inscribed in a circle of radius $r$ that has the maximum perimeter and the maximum area.
Getting Started
Think about what stays the same and what changes if you fix $c$ and vary $a+b$.
For the first part you have a right-angled triangle so you might try to use Pythagoras' Theorem which suggests working with $(a+b)^2$. The key idea is to maximise the area of the triangle.
To generalise this go from Pythagoras' Theorem to the Cosine Rule. Again use the area of the triangle. The key idea here is that if you fix $c$ and vary $a+b$ the angle $\angle ACB$ is constant.
The last part calls for a careful argument based on four applications of the second result.
Student Solutions
Congratulations to Curt, Reigate College and to Andrei, Tudor Vianu National College, Bucharest, Romania for you solutions to this problem
When AB is a diameter angle $ACB$ is 90 degrees so we can use Pythagoras' Theorem. The area of the triangle is given by $\textstyle{1\over 2}ab = \textstyle {1\over 2}ch$ where $h$ is the length of the perpendicular from $C$ to $AB$. Then
$$(a+b)^2=a^2+b^2+2ab=c^2+2ch.$$
Thus $(a+b)^2$ is a maximum when $h$ is a maximum and equal to the radius of the circle $\textstyle {1\over 2}c$ . So the maximum value of $a+b$ is $c\sqrt 2$.
Image
When $AB$ is not a diameter we have (using the Cosine
Rule):
$$\eqalign{ (a+b)^2 &= a^2 +b^2 + 2ab \cr &= c^2 +
2ab\cos \angle ACB +2ab \cr &= c^2 +2ab(1+\cos \angle ACB) \cr
&=c^2 +4ab \cos^2 \textstyle {1\over 2}\angle ACB.}.$$
As the area of triangle $ACB$ is given by $\Delta = \textstyle
{1\over 2} ab\sin \angle ACB$ we have
$$\eqalign { (a+b)^2 &= c^2 + {8\Delta \cos^2
\textstyle{1\over 2}\angle ACB \over \sin\angle ACB} \cr &= c^2
+ 4\Delta \cot \textstyle {1\over 2}\angle ACB }.$$
If we keep $A$ and $B$ fixed and vary $C$ then, as $c$ and
$\angle ACB$ are constant, and the area of the triangle $\Delta$ is
a maximum when $h$ is a maximum, it follows that $a + b$ is a
maximum when $h$ is a maximum, that is when $a=b$ and the altitude
of the triangle drawn from $C$ to $AB$ is a line of symmetry of the
triangle. In this case
$$a=b={c\over 2\sin \textstyle {1\over 2}\angle ACB}.$$
Conjecture: Let $Q$ be a variable cyclic quadrilateral in a
circle of radius $r$. Then the area and the perimeter of $Q$ will
be a maximum when $Q$ is a square; that is when each of the
diagonals of the quadrilateral is a diameter and each diagonal
bisects of the other diagonal at right angles.
Image
Teachers' Resources
The three parts of this question build on each other and require careful arguments based on simple algebra, geometry and trigonometry.
