Arithmagons
Can you find the values at the vertices when you know the values on the edges?
Problem
An arithmagon is a polygon with numbers at its vertices which determine the numbers written on its edges.
Check you understand how the values at the vertices determine the values on the edges in the arithmagons generated by the interactivity below, by clicking on 'New Numbers' and then on 'Reveal':
If you are given the values on the edges, can you find a way to work out what values belong at the vertices? Use the interactivity below to test out your strategies.
There are four different challenge levels to try.
Once you are confident that you can work out the values at the vertices efficiently, here are some questions you might like to consider:
- Can you describe a strategy to work out the values at the vertices irrespective of the values given for the edges?
- By looking at the numbers on the edges, how can you predict whether the numbers at the vertices will all be positive?
- By looking at the numbers on the edges, how can you predict whether the numbers at the vertices will all be whole numbers?
- What happens to the numbers at the vertices if you increase one or more of the numbers on the edges by 1? By 2? ... By n?
- What relationships can you find in square arithmagons? Or pentagonal arithmagons?
Here is a poster of this resource.
Getting Started
How does the sum of the numbers at the edges relate to the sum of the numbers at the vertices?
It might help to label the numbers at the vertices $A$, $B$ and $C$ and then express the edge numbers in terms of $A$, $B$ and $C$.
Student Solutions
Esther did some wonderful "detective work" and made a number of very useful observations:
1) The totals in the squares are double the totals in the circles. I think this is because each circle number is used twice to solve the puzzle.
2) If the numbers in the squares are all even, the numbers in the circles are either all odd or all even.
If the numbers in the squares are all odd, I cannot solve the puzzle with whole numbers. This is because an even number minus an odd number equals an odd number.
If you have two odd and one even in the squares then the numbers in the circles are either two odd and one even or two even and one odd.
However, if you have two even and one odd number in the squares you cannot solve the puzzle using whole numbers.
3) If you draw the lines of symmetry through a circle and the opposite square, the difference in the numbers in the squares on either side equals the difference in the numbers in the circles on either side.
Also the sum of the numbers on each line of symmetry is the same. This also works for decimals and negative numbers.
4) I found a rule for working out the numbers in the circles. You add the numbers in the squares next to it, subtract the number in the opposite square, and divide the answer by two. This is why you sometimes get decimals and negative numbers. I have only ever found one solution to each puzzle using my rule.
I think you can always get answers as long as you can use decimals and negative numbers using my rule as zero can always be made of +2 and -2 for example.
Harriet and Laura from The Mount School offered the following explanation:
We found that when you added together the numbers in the squares, (the ones already given) it totalled twice the accumulated amount of the numbers in the circles. The reason for this can be shown using algebra and is illustrated in the diagram below.
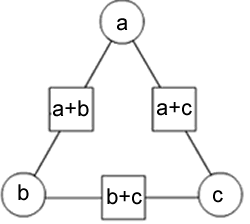
You can find the numbers being represented by $a$, $b$ or $c$ if you have numbers in the squares.
We will show this by finding b using an example found on the website:
Using the equation $(b + a) + (b + c) = 2b + a + c $
you can take away $a$ and $c$ to find $2b$:
$(2b + a + c) - (a + c) = 2b $
So $(b + a) + (b + c) - (a + c) = 2b $
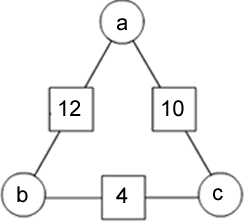
$2b = 12 + 4 - 10 = 6 $
$b = 3 $
This also works with negative numbers.
Robert from Leventhorpe School used a similar analysis:
To work out the formula for working out these arithmagons, we must first substitute the numbers as such:
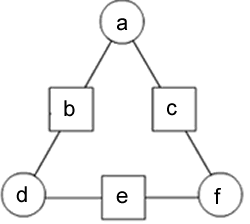
If we know $b, c$ and $e$, then we can say that
$a + d = b$,
$d + f = e$ and
$a + f = c$
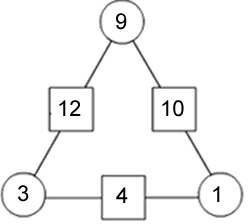
In the first one, $b = 12, c =10$ and $e = 4$,
so $a + d = 12$, $d + f = 4$ and $a + f = 10$
If we then add all of these together,
we get $(a+d) + (d+f) + (a+f) = 12 + 4 + 10 $
We do not need the brackets,
so we can make it $a + d + d + f + a + f = 26 $
This can be cancelled down to $2a + 2d + 2f = 26 $
If we then divide everything by $2$ we get $a + d + f = 13$.
Because we know that $a + d = 12$, $f$ must be $1$.
Since $d + f = 4$, $d$ must be $3$.
Finally, we can say that a must be $9$.
Double checking this, it works. Take a look:
Tom from Colyton Grammar School also used some algebraic thinking to analyse the problem:
If the circles were $z, y$ and $x$ from the top clockwise and the squares are $q, r$ and $p$ from the left clockwise then
$x + z = q$,
$z + y = r$
and $x + y = p$.
$q - r = x - y$
so $q + p - r = 2x$
so $x = (q + p - r) / 2$.
This means that $y = ( p + r - q ) / 2$
and $z = (q + r - p) / 2$, by symmetry.
Shaun from Nottingham High School came to the same conclusion:
It struck me this problem would be most easily investigated using simultaneous equations as a means of deriving a common rule for all arithmagons.
I will call the three circles of the arithmagon $a, d$ and $f$.
Hence, each squares can be expressed as the sum of two of the variables.
Since we have three variables, and three equations involving two of them each, we know it can be solved this way.
Some preliminary doodlings proved this to be true.
Let the squares be defined as follows:
(1) $a + d = b$
(2) $d + f = e$
(3) $f + a = c$

Therefore:
(4) $b + f = c + d$
(5) $b + f = e + a$
(6) $e + a = c + d$
From (4): $f = d + c - b$
Combining this result and (2):
$e - d = d + c - b$
$2d = e - c + b$
$d = (b + e - c)/2$
And so, using this formula, the value in a circle, when the three squares in the arithmagon are known, can be found.
Of course, the variable $b$ can be used to denote any of the three circles, and $x$ and $y$ the adjacent squares (does not matter which), and $z$ the opposite.
Following these rules, the formula can also be written as:
$a = (b + c - e) / 2$
$c = (c + e - b) / 2$
I think the process I have gone through above explains why all arithmagons can be completed - they all exhibit these attributes, and so can all be solved in the same way.
Lindsay's solution is here.
It explains why Tom from Cottenham Village College found that:
If you add up all of the numbers in the squares and halve it, then subtract the number on the opposite side to a circle (the number in the square) you will get the number that goes in the circle.
Aurora, from the British School in Manila, explained her strategy clearly:
Firstly, let's call the bottom left vertex z, the top one x, and the bottom right y.
Assume:
x+y= 17
y+z= 20
z+x= 15
If x+y is 17, and z+x is 15, the difference between z and y must be 2:
z+2=y
y+z= 20
z+z+2 =20
z=9
If z=9, y is 11 and x is 6
Here is how John and Karl, from King's School Grantham, explained how they derived a formula for finding the values of the vertices.
Here is how Charlotte, from Llandovery College, summarised two of the most popular strategies, and here is how Krystof, from Uhelny Trh in Prague, applied his strategy.
Here Connor uses an example to demonstrate his method for solving any arithmagon.
We also received good solutions to this problem from Leighton, Sia Jia Rui from Raffles Institution in Singapore, Bhavik, Brenna from Bream Bay College, Heer, Sarah & Heledd from St Stephen's Carramar in Perth, Alex and Luke from Llandovery College in Wales, Sam from Shrewsbury House School, Robert from West Hoathly Primary School, Amy from Hanham High School, Ryan and Alisha from Lacon Childe School, Lauren from St.Peters Primary School and Michael, Alexander, Jake, Hussein and Charlie from Wilson's School.
Teachers' Resources
Why do this problem?
Possible approach
- Are there any arithmagons that you haven't been able to complete?
- When do you need negative numbers?
- When do you need fractions or decimals?
- Does anyone have a strategy for completing the arithmagons?
- Can algebra help us?
Key questions
Is it always possible to find numbers to go at the vertices given any three numbers on the edges?
Possible support
To help students get started, use the interactivity on Level 1 to generate arithmagons which can be solved using only positive whole numbers.
Possible extension
Here are some NRICH magic graph challenges:
Magic letters
Olympic Magic
