Sets of Four Numbers
Problem
Miss Brown was working with Becky's group on numbers that share a certain property. She wrote twelve numbers on the board.

"You can all find a different set of just four numbers that go together," she said, "And they must have a proper mathematical name. They can't be just a set of numbers that you like!"
The children stared at the numbers. Alan put up his hand. "Like odd numbers?" he suggested.
"That's the right idea," said Miss Brown, "but you can't choose just odd numbers because there are more than four of them. You must use all the numbers in my list which fit your set. Anyone else got an idea?"
Becky put her hand up. "Numbers in the $5$ times table? There are four of those."
"That's right. But what would be a good name for them?"
"Multiples of $5$?" suggested Becky.
"Good," said Miss Brown and she wrote on the board:

Getting Started
Think of the properties of each of the numbers in turn.
Remember that each number can be in more than one set.
Student Solutions
There were so very many interesting ideas sent in for this challenge. Well done everyone!
We had solutions from:
Nadia and Lasata from Bentworth Primary
Anna, Jemma, Madeleine, Jessica and Linzi from Park View Community School
Phoebe, Joseph and Leigh from Newark Hill Primary School
Wiliam from Toot Hill
Chajicka and Demi-lee from Ricards Lodge High School
Hannah and Georgia from Penrhos College
Elm Park Maths Club
Year 8 at Dyffryn Taf
William from Barnton Community Primary School
Aman from Davidson Primary
Connie from Blackheath High School
Jaylyn
Year 5 maths club at Queens College Prep School
Hamish, Samuel and Rory from Rutherglen Primary School
Class 5S from Tenby Junior School
Ryan, Robbie and Georgia at Orchard Junior School
Vishaal from Brompton Manor
Shannon from St Julian's
Aporva
SHS Challenge Groupat Sutton High Junior School
Becky, Jacob and Katie from Tudhoe Grange
Simon from Dartford Grammar School
SaiSankalp from Roan Forest Elementary
Grace at Ninelands Primary School
Year 4/5 from Salisbury Heights (South Australia)
Samir from By Brook Valley
Year 6KM at Newton Primary School
Wazidur at Harrowden Middle School
Harry and Guy from St Michael's
Jessica from Jane Ryan School
Cameron, Kane, Jonathan, Aimee and Imogen from Falkland Primary School
Miss Parker's Class Aberdyfi
YemYem2 from Newstead
Imman from Foxborough
Oswald and Jimmy from Doncaster Gardens Primary School
Mark, Mekeela, Hannah, Sophie, Alexander, Jamie, Tom and Paula at Gledhow Primary School
Kelsey from Archbishop Beck
Kate, Alexander, Olivia and Thomas from Culford Prep
Mrs Lydford's Y6 Maths group from Balgowan Primary School
Norwich Numpties
Year 6 from Talycopa Primary
Miss Rowcliffe's Maths Class at Upton Heath Primary School
Mukul from The Grammar School at Leeds
Mrs Ferris' Maths Group at Wolfson Hillel Primary
Catherine, Kate, Lucinda and Ceciley from Wimbledon High School
Henry
Jazz and James from Woodstock C.E. Primary School
P5 and P6 Richmond School Ballygawley, Northern Ireland
Below you will see most of the ideas presented together, as there were many overlapping ideas:
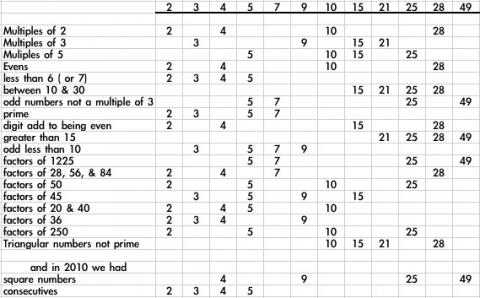
Well done to everyone!
