Cartesian Isometric
The graph below is an oblique coordinate system based on 60 degree
angles. It was drawn on isometric paper. What kinds of triangles do
these points form?
Problem
The graph below is a coordinate system based on $60$ $^\circ$ angles. It was drawn on isometric paper.
Image
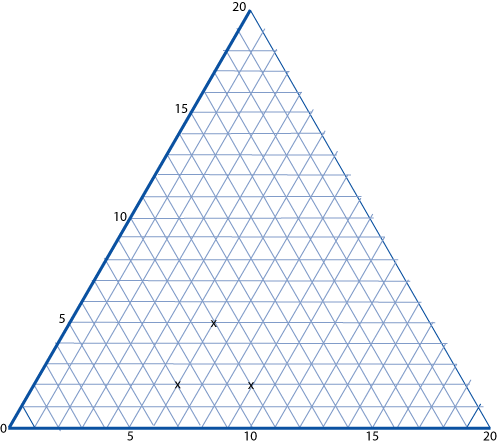
The marked points are $(6, 2)$, $(6, 5)$ and $(9, 2)$. When joined they form an equilateral triangle.
The following five sets of points are also triangles.
A. $(1, 13), (6, 8)$ and $(6, 13)$.
B. $(1, 1), (3, 3)$ and $(7, 1)$.
C. $(12, 1), (17, 1)$ and $(8, 9)$.
D. $(1, 10), (5, 2)$ and $(6, 6)$.
E. $(7, 5), (15, 4)$ and $(7, 11)$.
What kinds of triangles are they?
Can you work out any of the angles at the vertices?
Getting Started
Might it help to draw the triangle out on isometric paper?
What is the size of the angles created by the small triangles on the paper?
When you're working out the angles in the triangles, look carefully at how the sides cut through the grid triangles.
Student Solutions
Finding all the angles in these triangles is rather tricky, but well done to those of you who tried. Some of you measured the ones you couldn't work out using a protractor.
Georegie from St Lucifiers correctly identified the triangles and gave some of the angles, although you didn't say how you calculated them, Georegie:
A = Equilateral ($60$ $^\circ$, $60$ $^\circ$, $60$ $^\circ$)
B = Isosceles ($30$ $^\circ$, $30$ $^\circ$, $120$ $^\circ$)
C = Right angle scalene ($90$ $^\circ$, $30$ $^\circ$, $60$ $^\circ$)
E = Scalene
Ryo and Jake from Moorfield Junior told us that D is an isosceles triangle, but didn't give the angles - well done to you both. The angles in D were very tricky to calculate.
Teachers' Resources
Why do this problem?
This problem has an unusual context for coordinates which will provide an extra challenge when the group are working on coordinates or the angle properties of shapes.
Pupils need to be encouraged to look very carefully at the angles of the triangles. Isometric paper is almost essential.
Key questions
Do you think it would help to draw the triangle out on isometric paper?
What are the angles created in the small triangles on the paper?When you're were working out the angles in the triangles did you notice how the sides cut through the grid triangles?
Possible extension
Learners could make their own graph on isometric paper.
