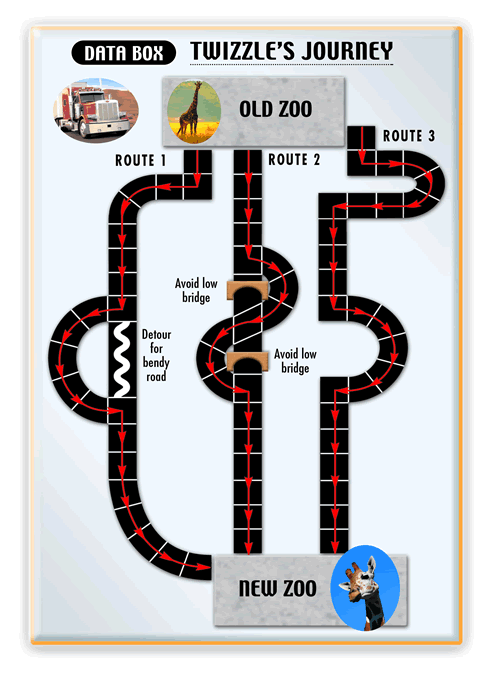
Twizzle's Journey

We had good solutions to this problem from several of you including Mollie who goes to St.Michael's C.of.E Primary School, Adam from Brayton College and Ruth from Swanbourne House School. Ruth said:

First we worked out which route was shortest:
Route $1$ has $22$ squares. Each square takes half an hour, so the total time will be $11$ hours.
Route $2$ has $19$ squares, so it will take $9\frac{1}{2}$ hours.
Route $3$ has $25$ squares, so it will take $12\frac{1}{2}$ hours.
So Route $2$ is the shortest. In a journey of $9\frac{1}{2}$ hours, there will need to be three stops. Each stop takes half an hour, so $3$ half hours = $1\frac{1}{2}$ hours.
This means the total journey time will be $9\frac{1}{2}$ hours $+ 1\frac{1}{2}$ hours $= 11$ hours.

Well thought out, Ruth.