Sending a Parcel
What is the greatest volume you can get for a rectangular (cuboid) parcel if the maximum combined length and girth are 2 metres?
Problem
Sending a Parcel printable sheet
The Post Office used to have a strange way of limiting the size of parcels. The maximum allowed was "6 feet combined length and girth". That meant you added together the distance round the middle of the parcel (that's the girth) and the length.
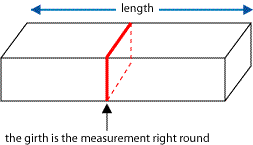
You could have sent a fishing rod very nearly 6 feet long and just a few inches round the girth!
Bringing the problem up-to-date, let's set the maximum combined length and girth to be 2 metres (which is a bit more than 6 feet).
What is the greatest volume you can now get for a cuboid parcel with whole centimetre dimensions?
Getting Started
How can you express the girth in terms of the width and breadth of the parcel?
How will you calculate the volume of the parcel?
How can you make the product of the width and breadth as large as possible for a given girth?
You might find it helps to use a spreadsheet.
Student Solutions
Ken from Blessed Robert Johnson School thought a cube would provide the optimum solution:
First we all clearly knows that a regular square will give the biggest area while the perimeter stays the same.
Therefore a regular square cube (length = width = height) gives the biggest volume.
To get the biggest volume I already know that the length, width and height have to be the same (to get a cube).
Let's call them A (use the same letter because they have the same value).
I know that 2(length + width) + height = or < 200,
so substituting A into the inequality I get:
5A = or < 200 which gives me A = or < 40
(this means if A is more than 40, then it will exceed the length + girth limit).
Say A is 40, then the volume will be 40 x 40 x 40 which gives 64000cm^3,
at the same time the length + girth is just 200cm which is just 2 metres.
So the biggest volume you can get is 64000cm^3 .
Elizabeth from Waverton CP School improved on this by finding two cuboids where the length is approximately twice the width and breadth (think of them as made up from two cubes stuck together):
Well done to you all.
Teachers' Resources
Why do this problem?
This problem gives practice in working with volume. It can be done by either trial and improvement or by using spreadsheets. It is a very good opportunity to see the value of using spreadsheets in solving problems.
Before tackling the problem, it might be valuable to investigate how the area of a rectangle can be maximised for a given perimeter.
Possible approach
Key questions
Possible support
Suggest trying Oh! Harry! which is a Stage 2 problem involving volume.
Possible extension
Learners could try Zin Obelisk, which is a similar problem.
