Coke Machine
The coke machine in college takes 50 pence pieces. It also takes a certain foreign coin of traditional design...
Problem
The coke machine in college takes 50 pence pieces. It also takes a certain (circular) foreign coin of traditional design.
Coins inserted into the machine slide down a chute into the machine and a drink is duly released.
How many more revolutions does the foreign coin make over the 50 pence piece going down the chute?
Getting Started
This is another tough nut and perhaps the diagram of the 50p piece will help.
Image
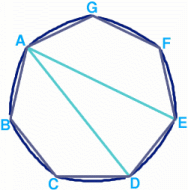
The 50p piece can roll in the same chute as a disc of radius $r$. Suppose the seven arcs forming the edge of the 50p piece (the arcs AB, BC etc. ) all have radius $R$ (where $R$=AD=AE=BE=BF...) then you need to find $R$ in terms of $r$. These seven arcs subtend angles of $2\pi /7$ at the centre of the disc and $2\pi /14$ at the opposite edge.
Student Solutions
We have Edwin Taylor, age 18 of the Leventhorpe School, Sawbridgeworth, to thank for the following solution.
Image
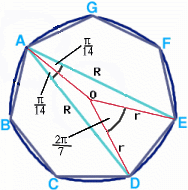
This is a diagram of the 50 pence piece with lines between $AE$ and $AD$ drawn in. We will say that these lines (and the others like them) have length $R$. Also, we will call the centre of the heptagon point $O$ and say that the lines $OA$, $OB$, $OC$ etc have length $r$.
____
If we assume the foreign coin has radius r, so is the same size as the dark blue circle pictured, then the chute could have width 2r, which will certainly be large enough for the 50 pence piece.
If the radius of this disc is $r$, then its perimeter (i.e. circumference) must be $2\pi r$. This is what the segment $OED$ with the arc $ED$ looks like:
Image
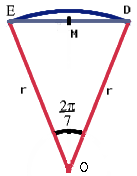
We know the angle EOD is ${{2\pi } \over 7}$ because it is one seventh of a complete revolution. The diagram also shows a point $M$ which is the midpoint of $ED$. Now if we look at the right angled triangle $EMO$, we can find out what $EM$ is:
Image
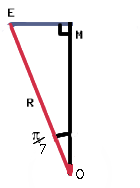
$$ EM = r\sin {\pi \over 7} $$ If we consider the segment $AED$, the arc $ED$ subtends an angle ${{2\pi } \over 7}$ at $O$ so angle $EAD$ is ${\pi \over 7}$ and angle $EAM$ is ${\pi \over {14}}$.
Image
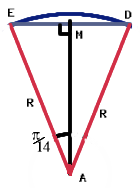
Using what we know about $EM$ we can find an expression for $R$ : $$ R = {{EM} \over {\sin {\pi /{14}}}} = {{r\sin {\pi /7}} \over {\sin {\pi /{14}}}}. $$ Now, if we use the trigonometric identity $\sin 2A = 2\sin A\cos A$ we get $$ R = 2r\cos {\pi /{14}}. $$ So, using the formula $S = r\theta $ that links the arc length ($S$ ) of a circle to the angle ($\theta $ ) that subtends it and the radius ($r$ ) of the circle, the length of the arc $ED$ is given by $$ ED = \left[ {2r\cos {\pi /{14}}} \right] \times {\pi /7}. $$ As the perimeter of the 50p is made up of 7 arcs of the same length as ED, the length of the perimeter of the 50p is $2\pi r\cos {\pi /{14}}$ . The ratio of the perimeter of the disc to the perimeter of the 50p piece is: $$ 2\pi r\ :\ 2\pi r\cos {\pi /{14}} = 1\ :\ \cos {\pi /{14}}. $$ So for every revolution of the 50p, the disc has gone 97.5% of a revolution, or every revolution the 50p gains on the disc by 1/40th of the discs revolution, or the 50p would do 40 revolutions in the space it would take the disc to do 39 revolutions.
____
However, the 50 pence piece actually has constant diameter $R$ (despite this being counter-intuitive). So the foreign coin could have radius $\frac{R}{2}$, and just fit into the same chute as the 50 pence piece. In this case, the disc has perimeter $\pi R$, which is (as previously shown) the perimeter of the 50 pence piece. So in this case, the two coins make the same number of revolutions.
