Something in Common

For this question you can only draw lines between points on the grid with integer coordinates, such as (6,-8,-2) or (3,7,0). You cannot draw lines between points that do not have integer coordinates e.g. (2.5,1,8) .

It is possible to draw a square of area 2 sq units on a coordinate grid so that two adjacent vertices are at the points (0,0) and (1,1) - see diagram below. In fact there are two such squares with sides $ \surd 2$ and area 2 square units - as shown.
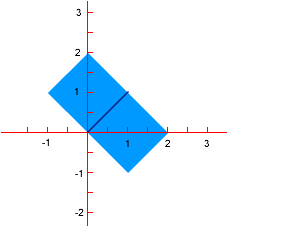
The Tilted Squares problem also investigates other squares you can draw by tilting the first side by different amounts. Here is a square with side: $ \surd 13$ and area 13 sq units.

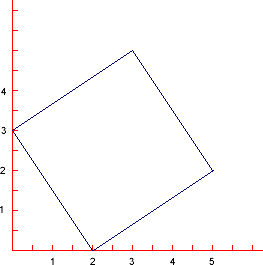
It is not possible to draw a square of area 3 sq. units on the grid. Try some squares for yourself and then explain why.

But is it possible to draw a square of area 3 sq. units in a 3D grid? First, you need to be able to make a side of length $ \surd 3 $. The line joining (0,0,0) to (1,1,1) has a length of $\surd 3$. How do I know?

Then you need three more sides all the same length that meet at the vertices and are at right angles to each adjacent side.

How many squares of area 3 square units can you find with this side in common, and what are the coordinates of their other vertices?