Coordinating classroom coordinates
I don't know about you, but as a teacher I used to love teaching coordinates. I frequently found that children who struggled with other branches of mathematics seemed to pick up this topic relatively easily. Coordinates lend themselves well to activities which pupils often find engaging. We're all familiar with traditional games like Battleships and you don't need to look far to find coordinate practice involving the creation of pictures, shapes or patterns. However, a more imaginative approach to the teaching and consolidation of coordinates is possible!
At a teacher conference I was lucky enough to attend the sessions given by Sue Lowndes and Elaine Sellars. They were full of ideas designed to promote and develop mathematical thinking in the classroom, ranging from investigational problems to end of term type games. The opening activities were all based on coordinates and it is these that I shall now describe. The appeal for me was the fact that everything was practical - we were physically participating in the maths ourselves.
Chairs were arranged in rows, a short distance apart, all facing the same way:
Image
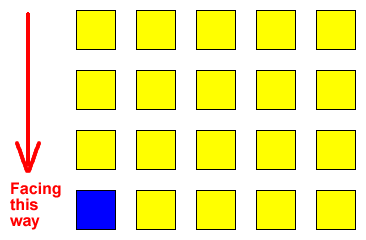
There were in fact a few more chairs than people so that when
we had all sat down, there were some empty. This was deliberate -
to make the activities more "interesting"! The "teacher" stood
facing us, although that is not strictly necessary.
We were told that one of the chairs (in the representation
above it would be the blue one) was in the first row and the first
column. From this information we could then work out which row and
column our particular chair was in. Row 1, column 1 was given the
position 1,1 so we could assign ourselves a set of numbers
too.
Instructions were called out and we responded accordingly. For
example:
- 4,1 and 2,3 stand up and swap places
- Stand up everyone in row 3
- Stand up everyone in column 5
Here it would be beneficial to explain to the children that
each chair is a point, having a particular position. The label
which each chair has depends on the reference point (in this case
the blue chair).
The reference point was then changed and the blue chair above
became (0,0). We adjusted our own coordinates accordingly. We began
with a similar place-swapping exercise to the one described above.
Then particular people were asked to stand, for example (1,0) (1,1)
(1,2) and (1,3). They were invited to:
- Say their own coordinates
- Notice what they all had in common i.e. first coordinate of 1
- Observe that they formed a straight line
This led on to the fact that because all the points on that
line have an x coordinate of 1, the line is called x = 1.
After a few practices of this, we were used to assigning a line its equation and the activities progressed into mirror symmetry. We were told that a particular line was the "mirror line". One point was called, that person stood up and then their reflection in the given line had to stand too. I have to admit that by this stage we had become much slower at jumping to our feet, not simply because of weary muscles but rusty brains too!!
The final challenge was to incorporate rotational symmetry. A point was chosen as the centre of rotation and everyone had to move into their new position after rotation of a given angle in a given direction. This was quite chaotic at first! We then tried another rotation but holding hands with two neighbours. This really emphasised the fact that we had all moved exactly the same amount in the same direction so that our spatial relationships with each other had not changed.
On a practical note, it may be helpful to place (0,0) in the diagonally opposite corner to the blue chair so that pupils have the origin at their left hand side. Depending on the space you have available, you may have to limit numbers and have a group of children at a time.
I came away itching to find a class to try this with! I am convinced that the "hands (or should that be bodies?) on" approach can only enhance our teaching methods. Obviously these activities are progressive so that you could not possibly include everything described in a single lesson, but do have a go and let us know how you get on. If you're feeling brave, why not extend it to 3-d?!!
Many thanks to Sue and Elaine for a wonderful session and allowing us to use their ideas.
