Leonardo of Pisa and the Golden Rectangle

Leonardo who?? You know, Leonardo the son of Bonacci. The one who lived from about 1170 to 1250 in Pisa, the Italian city with the famous Leaning Tower.


Here a picture of a statute of Leonardo that is in his home city. Do you recognise him now? (picture from the website of the School of Mathematics and Statistics University of St Andrews , Scotland)

Still puzzled?

Well, Leonardo is better known as Fibonacci. His statue is not as well known as his number sequence.

There is an Fibonacci association and even a journal dedicated to the sequence. But there was more to Fibonacci than a number pattern and counting breeding rabbits. If you don't know about the rabbits you can find out more at this website:

http://www.ee.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html#Rabbits

Fibonacci's number sequence (1,1,2,3,5,8,etc) has been discovered in some very interesting places. In branching plants, flower seeds and petal and leaf arrangements, on the outside of pineapples and inside apples as well as within pine cones. All involve the Fibonacci numbers - if you would like to discover how and why, Dr Ron Knott has the answers for you. You can do some Fibonacci puzzles if you visit the same site listed above.

If you investigate how the numbers of the sequence relate to each you will make another amazing discovery. Try dividing each number into the number that follows it, e.g. 2 into 3, 3 into 5, 5 into 8 and so on. Notice anything worth investigating further? Try finding the average of your answers. This is the type of strange phenomenon that intrigues mathematicians. If you have discovered a pattern to the answers, you have found an answer that is very close to what is sometimes known as the "golden mean".

http://www.vashti.net/mceinc/goldsqre.htm

Golden items are considered very valuable and quite rare. The "golden mean" has been a number used to investigate natural and man-made objects and the size of one part of the object to another part. When mathematicians examined what they considered to be perfect objects; a building like the Acropolis, a finely made and tuned violin, the human body, they discovered that the parts of the objects were in the same ratio as Fibonacci's numbers were to each other. They named this special relationship of the parts the "golden ratio".


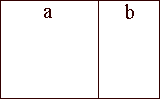
This diagram gives you an idea of the proportions of a Golden Rectangle . It is divided into two pieces, and the ratio of the two parts (a to b) is the Golden Ratio . If you investigate even further you will find that the two parts together (a+b) is the same ratio to just the left part (a)!

If the Golden Rectangle is divided into two pieces, like in the diagram, the result is a square (a) and another rectangle (b) which is the same shape but a different size (or similar) to the original Golden Rectangle . There are more 'golden shapes ' to be found in geometry and in nature. The nautilus shell or spiral, squares and triangles have all been investigated. There are more 'golden shapes ' to be found in geometry and in nature. The nautilus shell or spiral, squares and triangles have all been investigated.

http://www.vashti.net/mceinc/Unfold0.htm

The Golden Rectangle is said to be one of the most visually pleasing rectangular shapes. What do you think? Many artists think so and have used the shape within their artwork.

http://goldennumber.net

Whoever was the first to discover such intriguing evidence of geometry in nature, whether it was Fibonacci or not, must have been very excited about the discovery.