You may also like

problem icon

Hex

Explain how the thirteen pieces making up the regular hexagon shown in the diagram can be re-assembled to form three smaller regular hexagons congruent to each other.

problem icon

LOGO Challenge 6 - Triangles and Stars

Recreating the designs in this challenge requires you to break a problem down into manageable chunks and use the relationships between triangles and hexagons. An exercise in detail and elegance.

problem icon

Weekly Problem 18 - 2007

A regular pentagon together with three sides of a regular hexagon forma cradle. What is the size of one of the angles?

Weekly Problem 52 - 2012

Stage: 3 Challenge Level: Challenge Level:1


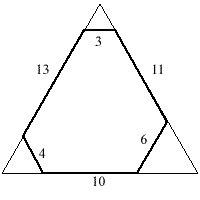
The diagram shows an irregular hexagon with interior angles all equal to 120 degrees made by cutting the corners off a piece of card in the shape of an equilateral triangle with sides of length 20 units.

An identical hexagon could also be made by cutting the corners off a different equilateral triangle.

What is the side length of this triangle?
 
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.  

This problem is taken from the UKMT Mathematical Challenges.

View the previous week's solution
View the current weekly problem
The NRICH Project aims to enrich the mathematical experiences of all learners. To support this aim, members of the NRICH team work in a wide range of capacities, including providing professional development for teachers wishing to embed rich mathematical tasks into everyday classroom practice. More information on many of our other activities can be found here.
Copyright © 1997 - 2012. University of Cambridge. All rights reserved.
NRICH is part of the family of activities in the Millennium Mathematics Project.