Heptagon Has
Weekly Problem 15 - 2012
How many of the five properties can a heptagon have?
How many of the five properties can a heptagon have?
Problem
A heptagon is a seven-sided polygon. What is the greatest number of the following properties that a single heptagon can possibly possess?
- Its interior angles add up to $900$ degrees
- It has exactly four acute interior angles.
- It has no obtuse interior angles.
- All its sides are equal.
- It has exactly one line of symmetry.
Student Solutions
It can possess all five properties.
Image
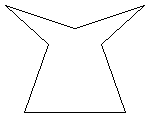
The description does not say that
heptagon has to be convex, i.e. all of its interior angles need not
be less than $180^{\circ}$. Since $(2 \times 7 - 4) \times 90
= 900$, the interior angles of all heptagons total $900^{\circ}$.
The creation of a heptagon with all the given conditions is
possible as the diagram shows. Notice that four of the interior
angles are acute and the other three are reflex angles.
