Centred
Weekly Problem 13 - 2012
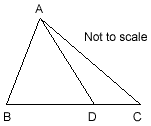
The diagram shows contains some equal lengths. Can you work out one of the angles?
The diagram shows contains some equal lengths. Can you work out one of the angles?
Problem
In the triangle $ABC$, $AD = BD = CD$. What is the size of angle $BAC$?
Image
Student Solutions
$\angle BAC = 90^{\circ}$
$A$, $B$ and $C$ are all equidistant from $D$ and therefore lie on a circle whose centre is $D$. $BC$ is a diameter of the circle and $\angle BAC$ is therefore the angle subtended by a diameter at a point on the circumference (the angle in the semicircle).
Alternatively, suppose $\angle ACD = x$. Then, $\angle BAC = x$ also, as $DAC$ is isosceles. This means $\angle CDA = 180 - 2x$ by angles in a triangle, so $\angle ABC = 2x$. Then, as $ADB$ is also isosceles, $\angle BAD = \angle DBA = \frac{1}{2}(180-2x) = 90-x$. Therefore, $\angle BAC = \angle BAD + \angle DAC = 90-x+x=90^\circ$
